19522x23=449006
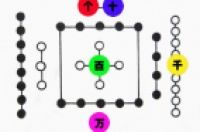
按被乘数摆棋子,如下图:
被乘数19522
根据乘以3的规则:
乘以3的运算规则
本位图变化如下:
被乘数:19522
乘以3(奇数)的被乘数的个位运动轨迹是“阴阳不变”,所以是奇数就是跳到下宫奇数,偶数就是跳到下宫偶数。
得出:
本位得数:37566
根据乘3规则:
如图:
乘3的进位图
我们观察被乘数19522,万位在水1不需进位,千位在火9需进二,百位在中5需进一,十位和个位都在火2不需进位。
因此实际进位图如下:
千位进二,百位进一,即:万位加2,千位加1,进位:21000
进位图和本位图合并如下,(熟练的情况下,实际是本位图挪好位置之后,直接加进位就可以了):
本位37566+进位21000
我们不需要按传统从小加起的原则,我们只需将重复的两个数加起来,就可以得出最终答案了,并没有顺序上的规定。
(千位,7+1=8,我们可以用加减7法则或者加减1法则,万位3+2=5也一样,我们可以用加减3或者加减2法则。)
得数58566
得出:五万八千五百六十六
剩下我们进行十位乘法,其实跟个位一样,只是进了一位:
(我们刚开始研究最好用两个盘,因为这样不容易混淆。)
根据乘2法则:
乘2法则
如图所示:
被乘数19522
百位是5,5的乘法是乘阴(偶数)去位(拿掉棋子),乘阳(奇数)不动位。现在我们是5乘以2,2为阴(偶数),所以我们将百位的棋子拿掉。如图所示:
本位得数28044
因为千位和百位进一,所以进位图如下:
进位11000
那么我们将进位的两图合并,实际是直接加在本位图就可以了
本位28044+进位11000
然后我们将相同的位数加起来,得出如下图:
本位28044+进位11000=得数39044
然后我们将这个图乘以十(万变十万,千变万,十变百,个变十):
39044乘以10后390440
再和刚刚算出的个位图相:叠加,(实际熟练的情况下直接在个位图上运算就可以了),如下图:
390440+58566
合并相同的数就变成了最终的答案,(其中百位5+4=9我们可以运用生数加土生数变成该宫成数的原理直接放个千位到成数位置)
390440+58566=449006
得出:四十四万九千零六
多位乘法按以上法则类推




