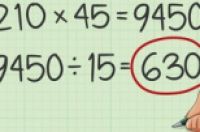
在本文中:列出数字的所有倍数使用素因式分解法使用网格法或梯形法使用欧几里德算法
倍数是一个数乘以整数得到的结果。一组数字的最小公倍数(简称为LCM)是这组数共有倍数中最小的一个数。要找出最小公倍数,你需要先确定各个数字的因数。求解最小公倍数的方法有很多。本文介绍的方法适用于求两个和更多数字的最小公倍数。
方法
1:列出数字的所有倍数
1:评估你要计算的数字。这个方法最适用于计算两个小于10的数字的公倍数,如果你面对的是比较大或比较多的数字,最好使用其它方法。
例如,我们需要找到5和8的最小公倍数。由于这两个数字都比较小,适合使用这个方法求出它们的最小公倍数。
2:从小到大列出第一个数字的几个倍数。用第一个数字乘以不同的整数就能得到它的倍数。也就是说,你可以直接查看乘法表,找到一个数的倍数。
例如,第一个数字5的倍数有5、10、15、20、25、30、35和40。
3:从小到大写下第二个数字的几个倍数。用相同的整数乘以第二个数字,得到几个倍数,来和之前的一组倍数进行比较。
在我们的示例中,数字8的倍数有8、16、24、32、40、48、56和64。
4:比较两个数字的倍数,找到其中最小的相同倍数。你可能需要列出更多倍数,来找到相同的那个倍数。你能找到的最小的相同数字就是最小公倍数。
例如,5和8的倍数里都有40,而且它是最小的相同倍数,所以40是5和8的最小公倍数。
方法
2:使用素因式分解法
1:评估数字。这个方法最适用于计算两个大于10的数字的公倍数,如果你面对的是比较小的数字,最好使用其它方法快速求出最小公倍数。
例如,如果你要找出数字20和84的最小公倍数,你可以使用这种方法。
2:将第一个数字进行因式分解。你可以将第一个数字因式分解成它的素数因数,得到的几个素数因数相乘,就能够得到原始数字。你可以画出因子树来将数字分解成素数。完成因式分解后,重新写出等式。等式的一边是被分解的数字,另一边是素数因数相乘。
例如,
{\displaystyle \mathbf {2} \times 10=20}
,
{\displaystyle \mathbf {2} \times \mathbf {5} =10}
,因此,20的素数因数有2、2、和5。重新写出等式,得到
{\displaystyle 20=2\times 2\times 5}
。
3:将第二个数字也进行因式分解。用相同的方式分解第二个数字,找到它的素数因数,各个素数因数相乘能够得到第二个数字。
例如,
{\displaystyle \mathbf {2} \times 42=84}
,
{\displaystyle \mathbf {7} \times 6=42}
, 以及
{\displaystyle \mathbf {3} \times \mathbf {2} =6}
。因此,84的素数因数有2、7、3和2。 重新写出等式,得到
{\displaystyle 84=2\times 7\times 3\times 2}
。
4:写下每个相同的素数因数,并将每个因数相乘,写成乘法等式。在你写下每个因数的同时,请在因式分解的等式中划掉对应的数值。
例如,两个数字拥有共同的因数2,因此,写下因数
{\displaystyle 2\times }
,并将每个因式中的2划掉。
两个数字还拥有另一个2作为共同的因数,因此,再写下第二个数字2,并写成两数相乘:
{\displaystyle 2\times 2}
,然后划掉因式分解式子里的另一个2。
5:将剩余的因数添加到乘法式子中。剩余的因数是指划掉公因数后,几个因式分解的等式中没有被划掉的因数。也就是两个数字的因数中不相同的那些。
例如,在等式
{\displaystyle 20=2\times 2\times 5}
中,两个2是两个数字共同的因数,因此你会划掉两个2。还剩下一个5,将5添加到上面的乘法式子中,得到:
{\displaystyle 2\times 2\times 5}
。
在等式
{\displaystyle 84=2\times 7\times 3\times 2}
中,你也划掉了两个2,还剩下了7和3,将这两个数字也加到乘式中,变成:
{\displaystyle 2\times 2\times 5\times 7\times 3}
。
6:计算最小公倍数。将上面写下的所有因数相乘,得到最小公倍数。
在我们的例子中,
{\displaystyle 2\times 2\times 5\times 7\times 3=420}
。因此,20和84的最小公倍数是420。
方法
3:使用网格法或梯形法
1:画一个井字形的网格。井字形的网格由两组平行线交叉组成,两组平行线彼此相互垂直,形成三行三列的网格,看上去像是手机或键盘上的井字键(#)。在网格最上方中央的方格内写下你的第一个数字,在网格右上角的方格内写下第二个数字。
例如,如果你想找到数字18和30的最小公倍数,请将18写在最上方中央的方格内,在网格右上角的方格写下30。
2:找到两个数字共有的因数。将这个数字写在网格左上角的方格内。最好使用素数因数,这会大大方便后续的计算,但是也不是必须的。
在求解18和30的最小公倍数例题中,由于18和30都是偶数,所以都能整除2,将2写在网格左上角的方格内。
3:用例题中的两个数除以共同的因数。将除得的商写在每个数字下面的方格中。进行除法计算就能得到商。
例如,
{\displaystyle 18\div 2=9}
,在数字18下面写下9。
{\displaystyle 30\div 2=15}
,在网格中30下面的格子里写下15。
4:找到两个商的公因数。如果两个商没有公因数,可以跳过这一步直接进入下一步。如果它们有公因数,请写在网格中央偏左的格子里。
例如,9和15的公因数为3,所以将3写在网格中央偏左的格子里。
5:用第一步得到的商除以新的公因数。将结果写在上一步结果的下面。
例如,
{\displaystyle 9\div 3=3}
,将3写在9下方的方格内。
{\displaystyle 15\div 3=5}
,将5写在15下方的方格内。
6:如果需要的话,继续扩展井字网格,画得大一点。然后按照上面的步骤计算除法,直到两个商没有相同的因数为止。
7:在网格第一列和最后一行的数字上画圈。圆圈连起来,就像是画出了一个大写的“L”字母。将圈出的所有数字相乘。
在我们的例题中,2和3位于网格的第一列,3和5位于网格的最后一行,写出数学式:
{\displaystyle 2\times 3\times 3\times 5}
。
8:完成乘法计算。将所有因数相乘,得到的结果就是原来两数的最小公倍数。
例如:
{\displaystyle 2\times 3\times 3\times 5=90}
。因此,18和30的最小公倍数是90。
方法
4:使用欧几里德算法
1:了解除法中的名词。“被除数”是除法运算中被另一个数所除的数;“除数”是被除数除以的数字;“商”是除法的最后结果;“余数”是整数被整除以后余下的数字。
例如,在方程
{\displaystyle 15\div 6=2\;{\text{余}}\;3}
:
15 是被除数
6 是除数
2 是商
3 是余数。
2:将方程改写成“商-余数”的形式。公式是 被除数 = 除数 × 商 + 余数。你需要用这个公式,根据欧几里得算法求出两个数字的最大公约数。
例如,
{\displaystyle 15=6\times 2+3}
。
最大公约数是两个数字公有的最大除数或因子。
使用本方法,你需要先求出最大公约数,然后通过它来找到最小公倍数。
3:用两个数字中较大的数字当被除数,使用较小的一个当除数。建立两个数字的“商-余数”方程。
例如,如果你要求210和45的最小公倍数,那么方程的形式是
{\displaystyle 210=45\times 4+30}
。
4:使用原除数作为新的被除数,使用余数作为新的除数。建立两个数字的“商-余数”方程。
例如,
{\displaystyle 45=30\times 2+15}
。
5:一直重复这个过程,直到最后的余数变成0。每一个新方程中,你都需要使用原除数作为新的被除数,使用余数作为新的除数。
例如,
{\displaystyle 30=15\times 2+0}
。因为,最后的余数是0,所以你不需要再继续除下去了。
6:找到最后一个方程中的除数。这个数字就是两个数字的最大公约数。
例如,因为最后一个方程
{\displaystyle 30=15\times 2+0}
中,除数是15,所以15就是210和45的最大公约数。
7:求出两个数字的乘积。用它们的乘积除以它们的最大公约数。最后的结果就是两个数字的最小公倍数。
例如,
{\displaystyle 210\times 45=9450}
。用乘积除以最大公约数,得到
{\displaystyle {\frac {9450}{15}}=630}
。所以,630就是210和45的最小公倍数。
小提示
如果你需要求多个数字的最小公倍数,那么上述的方法需要稍作更改。例如,要找到16、20和32的最小公倍数,请先使用上述方法求出16和20的最小公倍数(80)。再求出80和32的最小公倍数,最后计算结果是160。
最小公倍数有很多用途。最常见的用途是,当你计算分数的加减法时,几个分数的分母数字必须是相同的;如果分母不同,你需要将分子和分母同时乘以一个数,使得几个分数的分母变成相同的数字。最好的办法就是求出最小公分母(LCD),也就是分母的最小公倍数(LCM)。




