参照以下步骤计算圆面积。您也能学习到计算扇形面积的方法,扇形即圆形的一个切片,就像一个馅饼或比萨的切片一样。
方法
1:圆面积
1:计算圆半径。如果您只知道(或通过量度知道)圆直径(即圆的一侧到另一侧的距离),把圆直径除以二即可求得圆半径。正常圆形的半径总是其直径的一般。
2:了解计算公式。计算圆面积的公式为:面积等于pi乘以(r的平方)。
3:让半径乘以半径求出其平方值。例如,如果所求圆面积的半径为6厘米,则其平方值为36平方厘米。
4:把第3步中得到的结果乘以pi。(在"计算扇形面积"中也需采用该方法)。
如果您被要求"保留pi在结果中"或"需得出精确结果",则只需把pi保留在您的结果中(本例中,圆面积 = π36 cm^2。)如果您把pi换算为3.14,则所得结果只是一个近似值。把pi保留在结果中就是最精确的结果了,所有其他方法所得的结果均为近似值。
如果您被要求对结果进行四舍五入,把pi替换为3.14或使用您的计算器进行计算即可。例如:
方法
2:计算扇形面积
1:按照角度数确定扇形的大小。不幸的是,没有一种确定的方法能进行这一步骤。根据问题中的已知信息,可以采用不同的方法,但不存在通用的方法能让您在任何情况下都确定扇形的大小。
2:确定圆半径。同样地,圆半径总是等于直径的一半。
3:计算圆面积。请参考上述方法进行计算。
4:按比例计算出一个分数。您计算所得的分数应满足:
其分子为扇形圆心角度数,且
其分母为360°。
5:简化分数为最简分数。找出最小公分母以便简化分数。
6:把所得分数乘以圆面积。您的工作完成了!
除此之外(除了简化分数外),也可以把圆面积乘以扇形圆心角度数,再除以360°。
7:例如:
通过pi得出精确值的方法:
得出近似十进制值:
一般而言,您不会使用pi的整数部分作为计算系数。如果圆半径为3的倍数,则您的所得结果将会是截取自该分数和( )2的结果。您必须确定是否:(a) 保持分数的形式,保持pi作为pi的符号,并尽可能地进行交叉截取;或者(b)以3.14进行替换并通过除法完成计算。
方法
3:特殊圆形
1:以下特殊情况的处理方法:
有时您会遇到"位于正方形内部的圆形"。正方形的边长即等于圆形的直径。
另外,有时您也会遇到"一个正方形处于一个圆形的内部"。则正方形的对角线等于圆形的直径!
方法
4:量度圆形物体的直径
1:使用可伸缩的"卷尺",就像用于缝纫的那种,对物体的外部进行量度。确保以厘米进行量度。量度结果为物体的周长。将结果除以3.14可以得出直径的近似值。
2:如果您没有软性卷尺,也可以使用一条绳子量度物体的周长。然后用尺子量度绳子的长度,再除以3.14得出直径的近似值。
3:对于圆柱形物体,例如一个罐头,您可以使用您的"尺子"穿过罐头的顶部进行量度。保持一端固定,然后旋转另一端。继续旋转直到延伸至最远点为止。这就是该物体的直径。
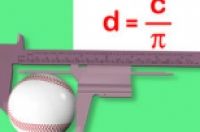
4:使用一套"卡尺"进行量度,这是一种用于量度物体外部尺寸的工具(看上去有一点像圆规),如果可能,您也可以使用这种工具对物体进行量度。仔细地量度,您将得出物体的直径。
小提示
使用计算器进行计算更方便。即使简单的4则运算计算器也能帮助您解决问题,但是更复杂的计算器能为您存储计算结果,便于日后的使用。您也可以使用计算机上的计算器。
别忘了您要对半径而非直径进行平方运算。
如果您需要帮助,可以求助朋友或家人,也可以进行网上搜索或查看数学书本。
请注意3.14只是pi的近似值;pi实际上具有无限的小数位,因此计算时请使用计算器。
把以上方法都记录在笔记本中。
警告
面对大尺寸的情况,很难通过量度得到准确值。在计算和量度时也应考虑这些因素。
计算扇形面积时,去掉扇形的弧形边,进而以其对应的三角形面积得出该扇形的面积,这种方法并不准确,尤其是在大圆形中。
你需要准备
铅笔
纸
计算器




