你是否需要知道如何计算串联电阻、并联电阻和串并混合电路的电阻?如果不想把电路烧了,那你的确需要知道!本文将向你展示如何仅用几个简单的步骤就完成计算。阅读以前要说明,电阻其实并没有“内”、“外”之分,文中提到的“内”和“外”只是一种表述方式,帮助新手理解连接的概念。
方法
1:何为串联电阻。串联电阻就是把一个电阻的“外端”连接到电路中另一个电阻的“内端”。每增加一个电阻,电路的总阻抗都会增加。
以串行方式连接的 n 个电阻的计算公式是:
Req = R1 + R2 + .... Rn
即所有串联电阻阻值相加。举例说明,想想如何计算图中所示电路的等价阻值
在这个例子中,
R1 = 100 Ω 和 R2 = 300Ω 相互串联。Req = 100 Ω + 300 Ω = 400 Ω
方法
2:并联电阻
1:何为并联电阻。当两个或多个电阻的“内端”彼此相连,“外端”也彼此相连时,即为并联电阻。
以并行方式连接的 n 个电阻的计算公式是:
Req = 1/{(1/R1)+(1/R2)+(1/R3)..+(1/Rn)}
这里举例说明,已知R1 = 20 Ω,R2 = 30 Ω且R3 = 30 Ω。
这3个电阻并联后的总阻值相当于:
Req = 1/{(1/20)+(1/30)+(1/30)}
= 1/{(3/60)+(2/60)+(2/60)}
= 1/(7/60)=60/7 Ω = 约 8.57 Ω。
方法
3:串并混合电路
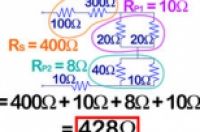
1:何为串并混合电路。混合电路就是串联电路和并联电路以任何方式的连接组合。想想如何计算下图所示电路的等价阻值。
可以看到,电阻R1和R2是串联的。因此其等价阻值(我们用Rs来表示它)就是:
Rs = R1 + R2 = 100 Ω + 300 Ω = 400 Ω。
接下来,我们看到电阻R3和R4是并行连接的。因此其等价阻值(我们用Rp1来表示它)就是:
Rp1 = 1/{(1/20)+(1/20)} = 1/(2/20)= 20/2 = 10 Ω
然后,我们看到电阻R5和R6也是并联的。因此其等价阻值(我们用Rp2来表示它)就是:
Rp2 = 1/{(1/40)+(1/10)} = 1/(5/40) = 40/5 = 8 Ω
那么现在我们就有了一个由电阻Rs、Rp1、Rp2和R7串联而成的电路。只需将其相加,即可得到原始电路的等效电阻R7。
Req = 400 Ω + 20Ω + 8 Ω = 428 Ω.
相关知识
了解电阻。每种能导通电流的材料都具有电阻系数,即这种材料对电流的阻抗。
电阻的衡量单位是 欧姆。欧姆的符号为 Ω。
不同的材料阻抗特性也不同。
举例说明,铜的电阻率为 0.0000017(Ω/cm3)
陶瓷的电阻率约为 1014(Ω/cm3)
数值越大,对电流的阻抗就越大。你看,铜的电阻率很低,所以常用在电线中。而陶瓷则相反,它的阻抗如此大,用作绝缘体最合适。
如何将多个电阻连接在一起,对电阻性电路的总体性能会产生很大影响。
V=IR。这就是欧姆定律,由格奥尔格•欧姆在18世纪初提出。如果你已知三个变量中的两个,就能轻易算出第三个。
V=IR: 电压 (V) 为电流 (I) * 电阻 (R)。
I=V/R: 电流为电压 (V) ÷ 电阻 (R)。
R=V/I: 电阻为电压 (V) ÷ 电流(I).
小提示
并联电路的等效电阻(Req)总是小于所有并联电阻中最小的;串联电路的等效电阻总是大于所有串联电阻中最大的。
记住,当多个电阻并行连接时,有多条通路可导通电流,因此总阻抗小于每条通路的阻抗。而当电阻串联时,电流需要通过每个电阻才能流通,因此单个电阻的加和才是串联总电阻。




