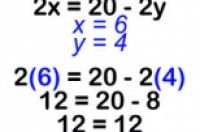
在本文中:解两边都含有未知数的方程[1]做一道例题做另外一道习题解含有两个未知数的方程解二元方程组参考
一开始,你可能觉得解两边都含有未知数的方程很吓人,但只要你学会移项(将未知数移到同一边)之后,一切都变得很好处理。这里,我们举几个例子,你可以在练习时看看。
方法
1:检查方程式。当解两边都含有未知数的方程时,我们的目标就是将所有未知数都移到其中一边。根据方程式的具体情况来决定解题的最佳方法。
20 - 4x = 6x
2:将未知数移到其中一边。你可以在两边加减公因式来实现移项(将未知数移到同一边)。你必须在两边都加或减公因式,这样方程两边才能平衡。选择方程中已有的公因式,如果可能的话,移项时,最好把未知数前面的系数化成正值。
20 – 4x + 4x = 6x + 4x
20 = 10x
3:通过除法来化简方程式。当未知数前仍然存在公因数时,用除法除掉这个公因数。同样,方程两边都要除掉相同的公因数,这样方程两边才会平衡。做到这一步,方程中的未知数就移到同一边了(完成移项),接下来你就可以轻松地解这个方程了。
20 / 10 = 10x / 10
2 = x
4:验算方程。 将算出来的未知数的值,代入到原有的方程中去验算(也就是用算出来的值代替原来的未知数)。如果方程两边的值相等,那么恭喜你,你的答案是正确的。
20 – 4(2) = 6(2)
20 – 8 = 12
12 = 12
方法
2:做一道例题
1:研究方程。当解两边都含有未知数的方程时,我们的目标就是将所有未知数都移到其中一边。对于有些方程来说,移项之前,你可能需要先进行其他步骤。
5(x + 4) = 6x - 5
2:如果需要的话,展开括号表达式。当解包含括号表达式的方程时,例如5(x + 4),你必须先利用乘法分配率展开括号表达式。这是移项之前的必要步骤。
5x + (5)4 = 6x – 5
5x + 20 = 6x – 5
3:将未知数移到一边。在将括号表达式解决掉之后,应用移项的标准方法将未知数移到同一边去:在两边加减公因式来实现移项(将未知数移到同一边)。你必须在两边都加或减公因式,这样方程两边才能平衡。选择方程中已有的公因式,如果可能的话,移项时,最好把未知数系数化成正值。
5x + 20 -5x = 6x – 5 -5x
20 = x – 5
4:运用加法或减法来化简方程式。有时候,加上某个数可以使得方程的一边只剩下未知数。注意,一定要在方程的两边都加上或减去同一个数,这样方程才能平衡。
20+5 = x – 5 +5
25 = x
5:验算方程。将算出来的未知数的值,代入到原有的方程中去验算(也就是用算出来的值代替原来的未知数)。如果方程两边的值相等,那么恭喜你,你的答案是正确的。注意,验算两次,确保没有算错哦。
5(25 + 4) = 6(25) – 5
125 + 20 = 150 – 5
145 = 145
方法
3:做另外一道习题
1:研究方程。当解两边都含有未知数的方程时,我们的目标就是将所有未知数都移到其中一边。对于有些方程来说,移项之前,你可能需要先进行其他步骤。
-7 + 3x = (7 - x)/2
2:将所有分数去掉。如果方程的某一边含有分数式,那么你需要利用乘法将分数式解决掉。同样的,你需要在方程两边都乘上同一个数,这样方程的两边才会平衡。
2(-7 + 3x) = 2[(7 – x)/2]
-14 + 6x = 7 - x
3:将未知数移到同一边(移项)。在方程的两边加上或者减去同一公因式。两边进行同样的加减。选择方程中已有的公因式,如果可能的话,移项时,最好把未知数前面的系数化成正值。
-14 + 6x +x = 7 – x +x
-14 + 7x = 7
4:通过加减法化简方程式。当含有未知数的一边还存在其他数字,利用加法或者减法将这个数字消除掉。你必须在方程的两边都加上或者减去这个数值,以保证方程两边的平衡。
-14 + 7x +14 = 7 +14
7x = 21
5:通过除法来化简方程式。当未知数前仍然存在公因数时,用除法除掉这个公因数。同样,方程两边都要除掉相同的公因数,这样方程两边才会平衡。做到这一步,方程中的未知数就移到同一边了(完成移项),接下来你就可以轻松地解这个方程了。
(7x)/(7)= 21/7
x = 3
6:验算方程。将算出来的未知数的值,代入到原有的方程中去验算(也就是用算出来的值代替原来的未知数)。如果方程两边的值相等,那么恭喜你,你的答案是正确的。
-7 + 3(3) = (7 – (3))/2
-7 + 9 = (4)/2
2 = 2
方法
1:研究方程。当方程含有两个未知数(无论是在同一边,还是在不同边),那么你将无法确切地算答案。你可以求解某个未知数,但你的答案却包含着另外一个未知数。
2x = 10 - 2y
2:求解 x。按照解包含一个未知的方程的方法来求解“x”。根据需要化简方程式并进行移项(不要考虑其他因素)。注意,下面的例子中,当解“x”时,把“y”看作你的答案。
(2x)/2 = (10 – 2y)/2
x = 5 - y
3:或者,求解“y”。按照解包含一个未知的方程的方法来求解“y”。根据需要,应用加法,减法,乘法、除法等化简方程。然后,在不考虑其他因素的情况下,将“y”移到方程的其中一边。注意,下面的例子中,当解“y”时,把“x”看作你的答案。
2x - 10 = 10 - 2y -10
2x – 10 = - 2y
(2x – 10)/-2 = (- 2y)/-2
-4x + 5 = y
方法
5:解二元方程组
1:研究方程组。如果你有一个包含不同未知数的方程组(多个不同的方程),那么你就可以解出每个未知数的值。在求值之前,确保将某个未知数移到方程的某一边。
2x = 20 - 2y
y = x - 2
2:将某个变量方程带入到另外一个方程中。如果某个等式还没有进行移项,那么先把那个等式移项。将某个未知数的值带入到另外一个方程之中(此时,这个未知数的值还是以等式形式出现。)这样的转化之后,其中一个等式就变成了一元方程(只有一个未知数)。
2x = 20 - 2(x - 2)
3:求解余下的未知数按照通常的方法,化简等式并移项。然后,你就可以解出等式中的未知数的值了。
2x + 2x = 20 - 2x + 4 + 2x
4x = 20 + 4
4x = 24
4x/4 = 24/4
x = 6
4:将刚刚解得的值代入到另外一个方程中。一旦你解出了其中一个未知数的值,你就可以把这个值代入到方程组中的外一个方程中,并解出另外一个未知数的值。通常来说,由于已经完成了移项任务,第二个变量的值很容易就可以算出来。
y = x – 2
y = (6) – 2
5:求解另外一个未知数的值。解决第二个未知数的值无需复杂的计算。
y = 4
6:验算答案。将两个未知数的答案分别代入两个方程中。如果两个方程的两边都相等,那么,两个未知数的答案都是正确的。
2(6) = 20 – 2(4)
12 = 20 – 8
12 = 12
你需要准备
铅笔
纸
计算器




