摘要 玄弧之比是一个近似值,e值是一个近似值,不是函数值的极限值都是近似值,近似值不能无限制地使用。
近似值的使用次数应该是有限的。比如:
1.1x1≈1;
1.1x2≈2;
1.1x3≈3
1.1x4≈4;
即1.1的倍数的近似值最多可以用4次,小白菜1.1元一斤,你买4斤4元卖家也许卖给你,你买5斤5元卖家肯定不会买给你了。
近似值的使用次数如果是无限的,那就会推导出一些错误的结论出来。
110=100, 220=200 330=300, 440=400 等
再看下面这些式子:
当n趋于无穷大时
1/n=0, 2/n=0, 3/n=0, 4/n=0 5/n=0 n/n=0 这些式子可以推导出什么结论来呢? 函数值不变原理。就看这一点,无限地使用近似值就闹出了一个天大的笑话。
公理:不是函数值的极限值都是近似值。 这一点只能让给读者来证明了。
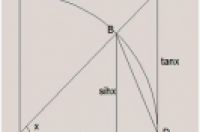
Sinx=AB, x=弧BD, tanx=DC, OB=1,
ΔDOB的面积<扇形DOB的面积<ΔDOC的面积
所以: sinx/2<x/2<tanx/2
即: sinx<x<tanx
从而有: sinx / x≠ 1
此处的x最小只能为无穷小,永远不能为零。
(2)e值是一个近似值
为什么说e值是一个近似值呢?
先看一个例子:
Y=x+2 x趋于2时y的极限
Y=2+2=4
y的极限就是x=2时y的函数值。
因为当n趋于无穷大时,1/n永远不等于零。这里暂时就把当n趋于无穷大时,1/n叫做无穷小。e值是1/n为无穷小时得到的极限值,我们需要的e值是1/n为零时的极限值。所以说e值是一个近似值。还有一点,这个无穷小的值究竟是多少还不知道,又怎能求出e的函数值呢?
e值是一个近似值,限制了e值的使用范围,这也是指数函数求导时代结束的一个原因。