文:岳峻 董永奇
对数平均数的不等式链的运用是近几年数学竞赛、名校模拟数学试题、高考数学真题的理论背景.
01:
对数平均引入与证明
先说重点:本文中涉及的对数平均不等式在考试中解答题不能直接用,需要给出证明过程
关于对数平均不等式的证明可以参考之前的文章《极值点偏移(五)——对数平均不等式》这里介绍一种几何证明 。
02:
借助于对数平均数的不等关系巧妙放缩
对数平均数的不等式链,提供了多种巧妙放缩的途径,可以用来证明含自然对数的不等式问题.对数平均数的不等式链包含多个不等式,我们可以根据证题需要合理选取其中一个达到不等式证明的目的.
评注 本题是高考试题的压轴题,难度较大,为了降低试题的难度采取多步设问,层层递进,上问结论,用于下问,其第二问是为第三问做铺垫的“梯子”,尽管如此,步骤依然繁琐,求解过程复杂,但我们这里应用对数平均数不等式链来证明,思路简捷,别具新意,易于学生理解、掌握.
又会得出怎样的结论呢?请看下例.
03:
多变量问题蕴含的对数平均数的不等关系
高考数学时常出现多变量的综合问题,且多出现在压轴题的位置,由于含有多个变量,使题目显得繁杂混乱,此类问题对学生的阅读能力、转化与划归的思维灵活性要求较高,许多学生面对此类问题往往一筹莫展,难以找到解决问题的突破口.如何从繁乱中理出头绪并顺利解决问题呢?
关于双变量也可参考这篇文章《导数压轴题中双变量的那些事儿》
破解此类问题,需运用转化与化归的思想,通过构造两个变量的比值(或差值)的函数,使之减少变量的个数,化归为我们所熟悉的一元函数,最后利用导数证明不等式.
评注 以此为背景的两个变量的不等式的证明问题,其解题策略:先将待证不等式逆推分析,进行等价转化,使得其中的两个变量的特征显现出来,然后利用换元法将两个变量的比值(或差值)作为新的一元变量.这种解题策略是转化与化归、消元与换元、构造与求导等基本数学思想方法的有机整合,因此此类问题是高考考查的重点.对数平均数不等式链的证明方法与本例的证明方法是一样的.
04:
利用对数平均数命题的变式探究
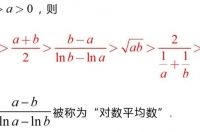
为了行文叙述的方便,将对数平均数不等式链中的
变式探究1:
变式探究2:
变式探究3:
变式探究4:
变式探究5:
变式探究6:
变式探究7:
变式探究8:
变式探究9:
变式探究10:
变式探究11:
变式探究12:




