题记:在上一篇,通过探索那道多解题的本质,后来引出了一个三爪图形。这个三爪图形在平时考试中是经常出现的,所以继续探索,发现以下有趣东西。
上篇回顾:
原题:
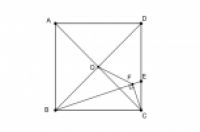
如图,正方形ABCD的边长是6,其中,CE=2,CF⊥BE,求OF的长
抽出此题的本质:
这是一个典型的三爪图。如图存在两个直角,可以得出三爪关系:
由旋转手拉手推理可得
FB - FC=根号2倍FO
用一句形象的话描述一下三爪定理:长爪与短爪之差等于根号2倍中爪
上图其实就是等腰直角三角形旋转过程中的一个特殊情形:
如果是一个30°的直角三角形呢?
因此,我画了一个369三角形,旋转试一试:
从这里可以看出三爪图只是两个相似直角三角形旋转过程中的特殊情形,也就是当点B,点D和点F三点共线时的情形。
如图,在Rt△ABC中,∠ABC=30°,点B, D, F,三点共线时即可得∠BFC等于90°
此时,三爪会存在什么关系呢?
通过旋转(△ABD相似于△ACF)推理可得:长爪 - 根号3倍短爪=2倍中爪(特注,长爪为FB,短爪为FC,中爪为FA)
如果是旋转到左边:
推理可得:
根号3倍长爪 - 短爪=2倍中爪(特注,长爪为DC,短爪为DB,中爪为DA)
这里如果再一般化一下呢?
此图还可以进行位似变换,呈现出不同的手拉手图形:
此图中可以研究很多东西。这里特看看形成三爪图时会存在哪些结论:
任意三角形中,若三边确定时,共顶点的两个三角形旋转时,若出现三点共线,此时三爪又会有什么规律呢?
如果OC=c, OB=b,BC=a; FO为短爪,FB为长爪,FC为中爪
那么依据旋转手拉手相似可以推得:长爪- b/c短爪=a/c中爪
整理得漂亮一点:c*长爪=b*短爪+a*中爪
这样就把前面提到的三爪图形引发的一些结论全都统一了!
不知您看到此推理过程时会做如何感想?反正我在推出时心情是洋洋得意,不过后来猛然发现,此定理其实就是托勒密定理的一个变形!(详细介绍看一题可破万题山(下篇))
顿时心情跌落谷底,原来自己绕了一个大圈子,其实也就那么简单!!!
不过在这里,通过探索也可以总结出一些有意义的东西:
若题目在以下情形出现三爪图时,都可以考虑用旋转手拉手模型求解,选择填空题直接用托勒密定理计算,(因为它们的本质都是旋转相似):
一、题目是以两个共顶点三角形旋转为背景:
(1) 命题角度是三点共线
(2) 命题角度是旋转过程中出现点重合,例如旋转过程中BF’和CF交点和点F重合时
(3) 两个顶角相等,例如上图∠BOC=∠BFC时
二、若题目以三角形外一点到三角形三个顶点的距离为背景:
(1) 两个侧边角相等,例如上图∠OBF=∠OCF时
(2) 两个顶角相等,例如上图∠BOC=∠BFC时
三、若题目以圆内接四边形为背景
另外,还发现一个挺有意思的东西:
河南2018年倒数第二题第三小问,考的就是这个三爪图。
题目:
题(3)中求解点C和点M重合时AC的长,实际上就是求解当三点B、C、D共线时短爪的长度。
此题存在两种情形:
情形一:
情形二:
很明显,里面存在三爪图,若能快速求解BC长度,然后利用三爪定理或者托勒密定理即可轻松求解。(当然此题方法还有很多)
不知命题人在命制此题时,是否考虑到了此模型。
突然有一种默然回首,那人却在灯火阑珊处的感觉:
我们在河南探讨14年的重庆中考题,竟然最后回到了河南18年的中考题。是不是有一种蓦然回首,那人却在灯火阑珊处的感觉。
想起辛弃疾那首词:
东风夜放花千树,更吹落,星如雨。
宝马雕车香满路。
凤箫声动,玉壶光转,一夜鱼龙舞。
蛾儿雪柳黄金缕,笑语盈盈暗香去。
众里寻他千百度,蓦然回首,那人却在,灯火阑珊处。
最后留一道思考题:
(原创)如图,已知AB=2, BC=5, AC=4,将△ABC以点A为位似中心,位似比为0.5进行缩小得到△AB"C",并使B"落在AB上。
(1)求△AB"C"的周长




