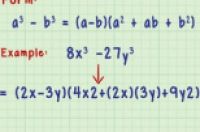
在本文中:分解数字和基本的代数式分解二次方程对其它形式的方程进行因式分解
在数学中,“因式分解”是指将一个数字或者表达式分解成几个数或者几个表达式的积的形式。因式分解是解决一些代数问题的常用方法,正确的进行因式分解是求解二次方程和其他多项式的基础。因式分解可以简化代数式,从而方便求解,而且还可以帮助你排除可能的答案,这要比直接动手计算再排除要快得多。
方法
1:分解数字和基本的代数式
1:对单个数字进行因式分解的定义。因式分解的概念很简单,但是在实际操作中,对复杂的方程进行因式分解却并不容易。因此,先从单个数字的因式分解开始,然后再应用到基本的代数式中,最后再来解决复杂的问题。一个数字的因子,是相乘之后的积为该数字的几个数。比如,12的因子是1, 12, 2, 6, 3, 4。因为1 × 12, 2 × 6, and 3 × 4 的结果都是12。
也可以这样理解,即一个数字的因子,是能整除这个数的数字。
你能求出60的所有因子吗?因为60可以被很多数字整除,所以60是很常用的一个数字(比如1小时有60分钟,1分钟有60秒,等等)。
60的因子是1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
2:能因式分解的变量表达式。就好像数字可以被分解一样,变量的常数系数也可以被分解。因此,你需要先找到变量的系数。对变量进行分解是简化代数方程的重要环节。
比如,12x可以看做是12和x的乘积。我们可以将12x写作3(4x), 2(6x), 等等,只要写成12的因数相乘的形式即可。
我们还可以将12的因数再进一步分解,换句话说,并不是分解到3(4x)或2(6x)就结束了,而是继续将4x和6x分解成3(2(2x)和2(3(2x)。显然,两个表达式的结果是一样的。
3:利用乘法分配律分解代数方程式。利用分解数字和带系数的变量的方法,你可以将数字和带系数的变量分解成含有相同因数的形式,从而简化表达式。通常,为了尽可能的简化,我们需要求两个数的最大公因数。而之所以可以这样化简的根据,是乘法的分配律,即对于任意的a, b, c, a(b + c) = ab + ac。
举例来说。对12 x + 6,进行因式分解。首先,先求出12x和6的最大公因数。6是最大的既可以整除12又可以整除6的数,所以可以化简成6(2x + 1)。
对于负数和分数也一样适用。比如,x/2 + 4,可以写成1/2(x + 8),,-7x + -21可以写成-7(x + 3)。
方法
2:分解二次方程
1:确定方程是二次方程 (ax2 + bx + c = 0)。二次方程的标准形式是ax2 + bx + c = 0,其中a, b, c是常数,并且a不为0(a可以是1或-1)。如果方程有1个变量(x),并且有1个或多个x的平方,你可以将等号一侧的变量移到等号另一端,让等号一端为0,另一端有ax2等。
比如,代数方程。5x2 + 7x - 9 = 4x2 + x - 18可以简化成 x2 + 6x + 9 = 0,转化成标准二次方程形式。
方程中有更高次的x项,比如x3,x4等。这样的方程是三次方程或四次方程,以此类推,除非大于2次的x项可以约去,否则这样的方程不是二次方程。
2:二次方程系数中,a = 1,可以因式分解成(x+d )(x+e),其中d × e = c,并且d + e = b。如果二次方程的形式是x2 + bx + c = 0 (换句话说,x2的系数为1),那么这样的方程可能(不保证)分解成这样的形式。找到两个数,它们的积是c,和是b,当你找到这样的两个数d和e之后,你就可以得到如下: (x+d)(x+e)。这两项的乘积就是原二次方程,换句话说,这两项就是二次方程的因式。
比如,方程x2 + 5x + 6 = 0。 3和2的乘积是6,3和2的和是5,所以方程可以写成(x + 3)(x + 2)。
根据具体方程的不同,最终结果的形式也有不同:
如果方程的形式是x2-bx+c,那么结果的形式是:(x - _)(x - _)
如果方程的形式是x2+bx+c,那么结果的形式是:(x + _)(x + _)
如果方程的形式是x2-bx-c,那么结果的形式是:(x + _)(x - _)
注意:上式空格中的数字可以是分数或小数,比如方程x2 + (21/2)x + 5 = 0的因式分解结果是 (x + 10)(x + 1/2)
3:可能的话,用试验法分解因式。信不信由你,对于一些简单的二次方程,一种简单的因式分解方法就是试验,将你认为可能的因式带入,直到你找到正确的因式为止。这样的方法叫试验法。如果方程的形式是ax2+bx+c且a>1,最终的因式分解的结果的形式可能是(dx +/- _)(ex +/- _),其中d和e是非零常数,且乘积为a。d或e可以为1(或者都为1),对于这个并没有硬性规定。如果d和e都为1,那么你可以使用上文的方法进行因式分解。
举个例子来说明。方程3x2 - 8x + 4,第一眼看上去很吓人。然后,当我们意识到3的因式只有2个(3和1)时,问题就变得简单了,因为我们知道最后的形式一定是(3x +/- _)(x +/- _)。在本例中,空格处都填-2,即为正确结果。-2 × 3x = -6x 和-2 × x = -2x;-6x和-2x的和是-8x;-2 × -2 = 4,所以,括号内的因式相乘的结果就是原式。
4:配方法。某些情况下,利用一些公式,二次方程可以很快很容易的因式分解。利用公式x2 + 2xh + h2 = (x + h)2,如果一个二次方程中,b的值是c的平方根的两倍,那么方程就可以转化成(x + (sqrt(c)))2的形式。
比如,方程x2 + 6x + 9符合上述要求。32 =9,3 × 2= 6。所以,方程的因式分解结果是(x + 3)(x + 3),或者(x + 3)2。
5:利用因式分解解二次方程。不论你的因式分解结果是什么,因式分解之后,你可以令每个因式的结果为0,从而解出x的值。由于你要找的x是能够让方程为0的值,所以一个能够让因式为0的x的值就是你要求的x。
让我们回到方程x2 + 5x + 6 = 0中。因式分解的结果是(x + 3)(x + 2) = 0。如果任意一个因式为0,那么整个方程的结果也为0,所以可能的x的解是让(x + 3) 和(x + 2)等于0的值。解得的结果分别是-3和-2。
6:检查结果,有时解出的结果并不是方程的解。当你求出了x的可能的值之后,将它们分别代入原方程,检查一下它们是否是方程的解。有时,你求出来的结果可能无法让原方程的值为0,这样的值要舍去。
将-2和-3代入方程x2 + 5x + 6 = 0。首先,代入-2:
(-2)2 + 5(-2) + 6 = 0
4 + -10 + 6 = 0
0 = 0。正确,所以-2是方程的解。
再代入-3:
(-3)2 + 5(-3) + 6 = 0
9 + -15 + 6 = 0
0 = 0。正确,所以-3也是方程的解。
方法
1:如果方程的形式是a2-b2,那么因式分解的结果是(a+b)(a-b)。只有两个变量的方程的因式分解结果和二次方程的基本形式的因式分解结果不同。对于任意的a2-b2,只要a和b不等于0,那么这样的方程总是可以化成(a+b)(a-b)的形式。
比如,方程9x2 - 4y2 = (9x + 4y)(9x - 4y)
2:如果方程的形式是a2+2ab+b2,那么它的因式分解结果是(a+b)2。注意,如果方程的形式是a2-2ab+b2,那么结果就是:(a-b)2。
方程2x2 + 16xy + 4y2可以写成2x2 + (2 × 2 × 4)xy + 4y2。方程满足上述的形式,所以我们可以确信,因式分解的结果是(2x + 4y)2
3:如果方程的形式是a3-b3,那么因式分解的结果是(a-b)(a2+ab+b2)。最后,值得一提的是,3次以更高次的方程是可以因式分解的,但是过程相对复杂费力一些。
比如,2x2 - 3y2的因式分解结果是(2x - 3y)(2x2 + ((2x)(3y)) + 3y2)
小提示
a2-b2是可以进行因式分解的, a2+b2 是不能因式分解的。
要记住如何分解常数,这有助于因式分解。
如果方程的形式是x2+bx+ (b/2)2,那么因式分解的结果是(x+(b/2))2。 (使用配方法得到的结果)
记住“0=0” (结果为0的特征)
你需要准备
纸
笔
数学书(有必要的话)