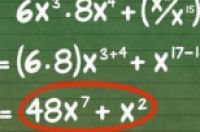
在本文中:合并同类项因式分解利用其它的化简技巧
学会如何化简代数式是掌握基本代数运算的关键部分,同时对于所有数学家来说,它也是一个非常有用的工具。化简可以让一个又长又复杂的代数式变得更简单更便于求解。基本的化简方法很容易学,就算是不喜欢学数学的人也能轻松学会。不需要特殊的数学知识,只需要简单几步,就可以化简几种常见类型的代数式。具体的方法请从下文的第一步开始学起。
步骤
重要概念
1:根据变量和指数定义同类项。在代数中,“同类项”是指含有相同的变量,相同指数的项。换句话说,同类项之间拥有相同的变量或几个变量,或者不含变量,并且相同变量的指数都一样,或者不含指数。而各项中的变量顺序无所谓。
比如,3x2和4x2是同类项,因为它们有相同的变量x,并且指数都为2。然而,x和x2就不是同类项,因为x的指数不同。再比如,-3yx和5xz也不是同类项,因为它们的变量组合不一样。
2:将数字因式分解成两个数字的乘积。因式分解是将一个数字分解成两个数字的乘积的形式。数字的因式分解结果不唯一,比如12可以写成1 × 12,2 × 6,和3 × 4,所以1,2,3,4,6,12都是12的因数。换种解释,一个数字的因数就是可以整除该数字的数。
比如,你想因式分解20,那么你可以将20写成4 × 5。
注意,还有变量的项也可以进行因式分解,比如20x,可以写成4(5x)。
质数是无法因式分解的,因为质数只能被它本身和1整除。
3:PEMDAS运算顺序。有时,化简代数式意味着要计算到求出结果之前的一步。所以,牢记运算顺序可以防止在化简过程中犯错。PEMDAS可以帮助你记住运算顺序 —— 每个字母对应了一种运算,按顺序依次是:
P代表括号(parentheses)
E代表指数(exponents)
M代表乘法(multiplication)
D代表除法(division)
A代表加法(addition)
S代表减法(subtraction)
方法
1:合并同类项
1:写出方程。最简单的代数方程中只包含几个变量,且系数为整数,也不含分数或根式等,求解这样的方程只需要简单几步。和计算大多数数学问题一样,化简代数式的第一步就是写出它。
下面以1 + 2x - 3 + 4x为例来说明。
2:找到同类项。写出方程之后,你需要找出方程中的同类项。不要忘了,同类项有相同的变量和指数。
比如,在1 + 2x - 3 + 4x中,2x和4x相同的变量x,且指数都为1;1和-3是常数项,不含有变量。所以2x和4x是同类项,1和-3是同类项。
3:合并同类项。找到同类项之后,你需要合并它们。将同类项相加(如果带有负号,那就减去),直到方程中不含同类项为止。
对于上面的例子来说
2x + 4x = 6x
1 + -3 = -2
4:用化简得到的各项组合成简化的表达式。合并同类项之后,用你新得出的几项重新组合成一个表达式。最终的表达式里的变量和原式是一样的,并且新的表达式和原式相等。
本例中,化简得到的两项是6x和-2,所以,新的表达式为6x - 2。它和原式(1 + 2x - 3 + 4x)相等,而且更短更容易处理。同时,新的表达式也更容易进行因式分解,下面我们就将提到因式分解,它也是重要的化简工具。
5:按照运算顺序合并同类项。在化简像上一个例子那样简单的代数式时,找到式中的同类项是很简单的。然而,在更复杂的,比如带有括号、分数和根式的代数式中,同类项并不是特别显眼。在这种情况下,你需要按照运算顺序对式中各项进行计算,直到最后式中只有加号和减号为止。
比如,方程5(3x-1) + x((2x)/(2)) + 8 - 3x。直接认为3x和2x是同类项,并把它俩进行合并是错误的,因为式中的括号表明还需要进行运算之后才能找到同类项。首先根据运算顺序,计算式中各项,如下:
5(3x-1) + x((2x)/(2)) + 8 - 3x
15x - 5 + x(x) + 8 - 3x
15x - 5 + x2 + 8 - 3x。现在,式中的运算符号只有加号和减号了,我们可以合并同类项了。
x2 + (15x - 3x) + (8 - 5)
x2 + 12x + 3
方法
2:因式分解
1:最大公因数。因式分解是通过提出所有项的共同因数从而化简代数式的一种方法。开始之前,需要先找到各项的最大的公因数,换句话数,就是找到最大的一个能够整除式中各项的数。
比如,9x2 + 27x - 3,注意到各项都可以被3整除,而且没有比3更大的数可以整除各项,所以,3就是最大公因数。
2:用式中各项除以最大公因数。接下来,用式中的每一项都除以你刚找到的最大公因数,最后得到的式子中,各项的系数都比原来小。
用上式各项除以最大公因数3。
9x2/3 = 3x2
27x/3 = 9x
-3/3 = -1
因此,新的式子是3x2 + 9x - 1
3:将原式改写成最大公因数和新式的乘积的形式。你得到的新的式子和原式并不相等,所以它并不是简化的结果。由于新式是提取了最大公因数后的结果,所以为了让化简之后的式子和原式相等,你需要让新式作为括号中的整体,再乘以最大公因数。
比如,3x2 + 9x - 1,先给它加上括号,然后再乘以最大公因数,得到3(3x2 + 9x - 1),该式和原式9x2 + 27x - 3相等。
4:使用因数化简分数。你现在也许想知道,为什么再提取最大公因数之后,还要再乘以它。事实上因式分解中是有很多小技巧可以化简代数式的。最简单的一个技巧就是利用了“分数的分子和分母同时乘以相同的数,分数的值不变”这一结论。如下:
原式是9x2 + 27x - 3,把它放到一个分母为3的分数的分子中,即(9x2 + 27x - 3)/3。我们可以用因式分解来化简它。
提取原式的最大公因数:(3(3x2 + 9x - 1))/3
注意到,分子和分母中都有相同的系数3,所以,分子分母同时除以3,有(3x2 + 9x - 1)/1
由于分母为"1"的分数和分子相等,所以原分数可以化简成3x2 + 9x - 1
方法
3:利用其它的化简技巧
1:除以相同的因数化简分式。如果,分子和分母有相同的因数,那么我们可以从分子和分母中同时除以它。有时我们需要对分子、分母,或者分子和分母进行因式分解,才能找到共同的因数,有时只需要观察就能找到相同的因数。要注意的是,有时你可以用分子中的各项除以分母,来得到简化的代数式。
下面举一个因数并不复杂的例子,(5x2 + 10x + 20)/10,即使5x2中的系数“5”比10小,10并不是5的因数,但是我们还是可以用分子中的每一项除以10来得到化简的代数式。
除以10的结果是((5x2)/10) + x + 2。我们可以将它改写成(1/2)x2 + x + 2
2:利用因数中的完全平方数化简根式。带有根号的表达式称为根式。提取根号下的完全平方数,并将它的平方根写在根号前面,从而化简根式。
比如,√(90)。将90看作是9和10的乘积,其中9是完全平方数,它的平方根是3,然后将3从根号下提出来。就是说:
√(90)
√(9 × 10)
(√(9) × √(10))
3 × √(10)
3√(10)
3:两个指数相乘时,将它俩的指数相加;两个指数相除时,将它俩的指数相减。有些代数式中,需要计算指数的乘积或商,此时,不用进行复杂的计算,只需要在乘的时候把指数相加,在除的时候把指数相减就可以了。这也适用于化简表达式。
比如6x3 × 8x4 + (x17/x15)。前后两部分需要分别计算指数的乘法和除法,而我们所要做的就是,对指数做加法和减法。过程如下:
6x3 × 8x4 + (x17/x15)
(6 × 8)x3 + 4 + (x17 - 15)
48x7 + x2
下面是对于这种做法的解释:
指数的乘法就是表示一长串非指数部分的乘积,比如,由于x3 = x × x × x,x 5 = x × x × x × x × x,所以x3 × x5 = (x × x × x) × (x × x × x × x × x),即x8。
同理,指数的除法就是表示一长串非指数部分的商。x5/x3 = (x × x × x × x × x)/(x × x × x)。由于分子和分母可以约去相同的因数,因此最终剩下两个x的乘积,即x2
小提示
化简代数式并不是很容易,但是一旦你掌握了它,你将会受用终身。
需要时可以请求别人的帮助。
要时刻记得,所有的数字前都有正号或负号,这样你就不会有“我该写什么符号”的疑问了。
警告
不要随便添加不存在的数字、指数或运算符。
不断寻找同类项,不要被指数所迷惑。




