收集数据后,你要做的第一件事往往就是对它进行分析。这通常都免不了要计算均值、标准差和标准误差。本文将向你展示如何计算。
方法
1:数据
1:获得一组你想要分析的数据。这些信息也称为样本。
例如,一个由5个学生组成的班级接受了一次测试,测试结果为12, 55, 74, 79和90。
方法
2:均值
1:计算均值。把所有数值相加,再除以总体大小:
均值 (μ) = ΣX/N,这里的 Σ 是求和(加法)符号, xi 是每个单一数值,而N则是总体大小。
在上例中,均值 μ 就是 (12+55+74+79+90)/5 = 62。
方法
3:标准差
1:计算标准差。它表征总体的分布情况。 标准差 = σ = sqrt [(Σ((X-μ)^2))/(N)].
对以上给出的例子,标准差是 sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4。(注意,如果要求样本的标准差,则应除以n-1,即样本大小减1。
方法
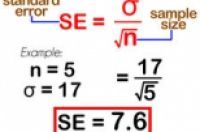
1:计算(均值的)标准误差。它表征的是样本均值与总体均值的近似度。样本越大,标准误差就越小,样本均值与总体均值也就越接近。将标准差除以样本大小N的平方根即可得出标准误差。标准误差 = σ/sqrt(n)
就以上的例子而言,如果从一个有50名学生的班级中抽取5个学生做样本,而50名学生的标准差为17 (σ = 21),则标准误差即为 17/sqrt(5) = 7.6。
小提示
均值、标准差和标准误差的计算对于分析正态分布的数据最有用。距离中心位置1个标准差的范围覆盖了约68%的数据,距离其2个标准差的范围覆盖了95%的数据,而3个标准差能覆盖99.7%的数据。随着样本大小的增加,标准误差会变小(分布范围变窄)。
易用在线标准差计算器
警告
仔细检查计算。计算中很容易出现失误,或是输入错误的数据。




