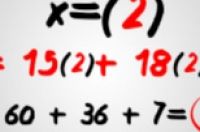
求多项式函数的微分可以得出该曲线的斜率。你只要将每一项的指数和系数相乘,将原项降低一次,除掉常数项即可。下面教你如何分解成数个简单的步骤来求微分。
步骤
1:找出变量项和常数项。变量项就是含有变量的项,常数项则是只有数字的项。找出 y = 5x3 + 9x2 + 7x + 3的常数项和变量项。
变量项:5x3、 9x2、 7x
常数项: 3
2:将每各变量项系数乘以指数。得出新一项的系数。得到这个积以后,将系数放在对应项前。下面是过程:
5x3 = 5 x 3 = 15
9x2 = 9 x 2 = 18
7x = 7 x 1 = 7
5x3 = 5x2
9x2= 9x1
7x = 7
4:把原系数和指数替换为新的项。你只要将原来变量项的地方替换成新的项即可。常数项求导是0,因此可以忽略掉这个常数项3。
5x3 变为 15x2
9x2 变为 18x
7x 变为 7
得到y = 5x3 + 9x2 + 7x + 3 求导结果 y = 15x2 + 18x + 7
5:得出确定x值的导函数值。要用x找出y的值,就把所有的x替换成确定的x值,然后解出来即可。比如想要找出x = 2 的函数值,替换x就可以得出答案了:
2 --> y = 15x2 + 18x+ 7 = 15 x 22 + 18 x 2 + 7 =
y = 60 + 36 + 7 = 103
x = 2 时函数值是 103
小提示
这里介绍的就是微积分次数法则:d/dx[axn]=naxn-1
注意导数的定义是: lim as h->0 of [f(x+h)-f(x)]/h
找不定积分也是同样方法,不过是步骤反过来而已。假设有12x^2 + 4x^1 +5x0 + 0 只要把指数加1,然后用系数除以变化后的指数,得到 4x3 + 2x2 + 5x1 + C ,这里的C 是常数,这里你是不能知道常数项是多少的。
注意只有在指数是常数的时候才能用此法则。比如d/dx xx 不是x(xx-1)=xx, 而是x^x(1+ln(x))。 xn 只有在 n是常数的时候才能用次数法则。
碰到负指数也不用担心,方法一样!比如有x-1,则得到 -xn-2, x1/3 则得到 (1/3)x(-2/3)