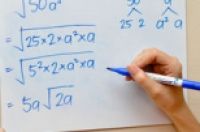
在本文中:完全平方数完全立方数不能完全化简的根式含有变量的根式化简含有数字和变量的根式
根式就是含有根数的代数式。可能是平方根、立方根或任何其他的根。简化根式可以方便解题,也可以尽量简化被开方数(根号内的数)。想知道如何用多种方式化简根式,下面教你。
方法
1:完全平方数
1:把任何含完全平方数的根式化简。完全平方数是一个数乘以自己得到的数,比如81就是9*9得到的。要简化,直接去掉根号,换成平方根数即可。
比如121就是完全平方数, 11 x 11= 121 你可直接把根号移掉,写成11就可。
要想更简单点,你要记住下面的头十二个数的完全平方数:1 x 1 = 1, 2 x 2 = 4, 3 x 3 = 9, 4 x 4 = 16, 5 x 5 = 25, 6 x 6 = 36, 7 x 7 = 49, 8 x 8 = 64, 9 x 9 = 81, 10 x 10 = 100, 11 x 11 = 121, 12 x 12 = 144
方法
2:完全立方数
1:把任何含完全立方数的根式化简。完全立方数是一个数连续两次乘以自己而得到的数,比如27就是3*3*3得到的。要简化,直接去掉根号,换成立方根数即可。
比如 512 就是完全立方数,因为8 x 8 x 8=512。 因此512的立方根就是8。
方法
3:不能完全化简的根式
1:把被开方数拆成自己的乘数。乘数是相乘得到目标数的数字。比如5、4是20的一对乘数,要把不能完全化简的根式中的数拆分成所有可能的乘数组合(太大的话就尽量多想),直到有完全平方数为止。
比如试着把所有的45乘数列出: 1, 3, 5, 9, 15, 和 45。 9 是一个乘数 ,亦是一个完全平方数。 9 x 5 = 45
2:把任何是完全平方数的乘数移出来。9是完全平方数(3*3),就把3提出来,根号里保留5。如果要把3放回去,就求平方得9再和5相乘得45。3根号5是根号45的简化说法。
方法
4:含有变量的根式
1:找出完全平方式。a的二次方的平方根就是 a, a的三次方的平方根就是 a乘以根号 a。因为你加了个指数,用根号a乘以a就相当于根号下的a的三次方。
因此这里的完全平方数就是“a”的平方。
2:把任何含有完全平方数的变量提出来。现在把a的平方提出来,变为a,放在根号左边,得到a三次方的平方根是a根号a
方法
5:化简含有数字和变量的根式
1:如果根式含有平方数,也含有变量的平方,则只要找出完全平方数,然后找出变量中的完全平方式,然后把根号去掉,得到平方根数。我们这里看看36*a^2的平方根。
36是完全平方数,因6 x 6 = 36
a的平方就是完全平方式,因为就是 a平方所得。
目前你已经把数字和变量变为平方根了,下一步就是把根号去掉,留下平方根。36 x a2的平方根就是 6a。
2:如果不是完全平方式,怎么做?下面我们把表达式分解成数字和变量两部分。分别找出两部分的完全平方数(式)。然后把可以提出来的提出来。下面我们做50*a3的平方根。
把50分解找出完全平方数。 25 x 2 = 50 , 25是个完全平方数( 5 x 5 = 25) 。根式中可以提出 5,然后里面剩下2。
把a的三次方中完全平方数找出来。a的三次方就是a的平方乘以a,a的平方就是完全平方式。提出a,剩下一个根号内的a。
把所有的东西合并起来。只要把之前提出来的、剩在根号里的都保持原样,然后合并起来(相乘)就可以 。 5 根号2和a根号a 合并得到5 x a 根号2 x a'.'
小提示
有的网站可以帮你化简根式,你可以查查相关的网站。只要输入等式,按回车就会得到化简的答案了。




