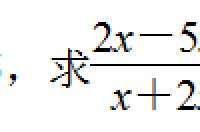
在最近的分式教学中,分式运算求值成了许多同学学习的难点.的确,这部分内容的求值方法灵活多变,又经常与完全平方公式等结合,技巧性很强.两年前,笔者曾经专门设置了一个专题《八下第四讲 5种方法,10道例题,分式求值技巧大揭秘》,本讲在此基础上进行补充.
一、经典再现
例1:
分析:
本题,在《八下第四讲 5种方法,10道例题,分式求值技巧大揭秘》中,我们用了整体同除法,其实还可以对已知条件进行通分,找出xy与x+y的数量关系,从而整体代入.
解答:
例2:
分析:
本题,在《八下第四讲 5种方法,10道例题,分式求值技巧大揭秘》中,我们用了整体同除法,其实还可以先求已知条件的倒数,找出x的倒数与y的倒数的和,y的倒数与z的倒数的和,z的倒数与x的倒数的和,将所求的分式也求其倒数,从而代入求解.
解答:
例3:
分析:
本题,在《八下第四讲 5种方法,10道例题,分式求值技巧大揭秘》中,我们用了特殊值法,但其实,也可以用a的代数式表示b,代入求解.
解答:
例4:
分析:
本题出现了等比,那应该选择设k法,但值得注意的是,最后的答案可能不止一解.
解答:
例5:
分析:
本题可以从去分母的角度入手,得到4x+1与含参数A、B的代数式相等的一个式子,则这个含参代数式的一次项系数是4,常数项是1,继而利用待定系数法,得到关于A、B的二元一次方程,从而求出A,B的值.
解答:
二、新题突破
例1:
分析:
本题,目前我们是无法求出x的具体的值,则只能从整体思考,能提公因式的先提公因式.
解答:
例2:
分析:
解答:
例3:
分析:
本题中,应该先将分子分母凑出一个整数,然后将剩余部分的分式转化为整数的形式,关注分母是分子的因数,同时要考虑x为整数.
解答:




