利用圆的周长和面积竟然可以计算如此复杂的图形,分割法的妙用。大家好我是小梁老师,这节课我们继续学习复杂图形的周长和面积。
难题点拨①
解题分析:我们知道圆环的面积等于外圆面积减去内圆面积,但是这个题目中外圆和内圆大的半径都没有给出,所以需要间接的去求圆环面积。
设外圆半径是R,内圆半径是r,根据题中条件得,图中阴影部分的面积可以表示为R²-r²=100平方厘米。
而圆环的面积为:
πR²-πr²=π(R²-r²)=3.14×100=314(平方厘米)
想一想做一做以下对应题目:
难题点拨②
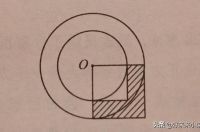
下图中,阴影部分的周长是14.28分米,阴影部分的面积是多少平方分米?
解题分析:观察图中,阴影部分的周长由圆的两条半径和圆周长的1/4组成,圆周长1/4可由圆的半径表示出来。因此,可设出圆的半径,列方程求出半径,再求阴影部分的面积。
解:设圆的半径为r,
则圆周长的1/4为1/4×2πr=πr/2
所以阴影部分的周长可以表示为:
2r+πr/2=14.28
解得r=4
阴影部分的面积就是:3.14×4²÷4=12.56(平方分米)
答:阴影部分的面积是12.56平方分米。
想一想做一做以下对应题目:
1.有一个半圆形零件,周长是25.7厘米,这个半圆形零件的面积是多少平方厘米?
2.将一个圆剪拼成一个近似的长方形(如下图),已知周长增加了10厘米,求圆的面积。
3.下图中,已知半圆的周长是10.28厘米,求阴影部分的面积。
难题点拨③
右图的中间是一个边长为3厘米的正方形。整个图形的面积是多少平方厘米?
解题分析:这个图形实际上是由一个正方形和
4个1/4圆组成的,它的面积就是一个正方形与4个1/4圆的面积之和。
4个1/4圆正好是一个完整的圆,这个圆的半径是3厘米,面积是3.14×3²=28.26(平方厘米)。
想一想做一做以下对应题目:
1.求下面各图中阴影部分的面积。(单位:厘米)
2.求下面各图中阴影部分的面积。
难题点拨④
将三根一样粗细的圆木像下图那样用铁丝在两头各捆一圈,如果每根圆木横截面的直径都是3分米,那么至少需要多长的铁丝?
解题分析:这个题目,我们在原图上做一些辅助线就可以看出解题思路了。
从图中很容易看出,铁丝的长正好是一个圆的周长,加上三条直径的和。
一个圆的周长:3.14×3=9.42分米
铁丝的长度:9.42+3×3=18.42分米
答:铁丝的长度至少18.42分米。
难题点拨⑤
下图中四边形ABCD是边长为1厘米的正方形、求阴影部分的周长。
解题分析:从图中可以看出阴影部分的周长是由①②③④四个扇形的弧长外加扇形④的半径减一组成。
扇形①的弧长:2×3.14×(1+1)÷4=3.14厘米
扇形②的弧长:2×3.14×(1+1+1)÷4=4.71厘米
扇形③的弧长:2×3.14×(1+1+1+1)÷4=6.28厘米
扇形④的弧长:2×3.14×(1+1+1+1+1)÷4=7.85厘米
所以阴影部分的周长是:
3.14+4.71+6.28+7.85+(1+1+1+1)=25.98厘米
答:阴影部分周长是25.98厘米。
难题点拨⑥
一个石英钟的时针长4厘米,经过12小时,石英钟的时针的针尖所走过的路程是多少厘米?
解题分析:十二小时时针刚好转过360°,也就是时针针尖的轨迹是个圆。这个题目就是让我们求一个半径是4厘米的圆的周长。
3.14×4×2=25.12厘米
答:12小时后,时针走过的路程是25.12厘米。
难题点拨⑦
如图,大圆直径为30cm,4个小圆的直径都是大圆直径的一半,求阴影部分的面积。
解题分析:这个题目主要用到分割法,将原图分割后,再重组图形,刚好是一个正方形,如下图所示:
所以阴影部分的面积是30×30÷2=450(cm2)
难题点拨1想一想做一做
1.3.14×200=628(平方厘米)
2.设大正方形的边长是A,小正方形的边长是a,那么大圆半径是A/2,小圆半径是a/2。
由题意知:A²-a²=100平方厘米
圆环的面积是:
3.14×(A/2)²-3.14×(a/2)²=78.5(平方厘米)
3.设大圆半径为R,小圆半径为r。
由题意知:R²÷2ーr²÷2=(R²-r²)÷2=25(平方厘米)
圆环的面积是:3.14×(R²-r²)=3.14×25×2=157(平方厘米)
难题点拨2想一想做一做
1.设半圆形零件的半径是r,依据题意列方程。
2r+2π×1/2=25.7解得r=5
半圆形零件的面积是:1/2×3.14×5²=39.25(平方厘米)
2.3.14(10÷2)²=78.5(平方厘米)
3.设半圆的半径是r。
2r+1/2×2πr=10.28
解得r=2
阴影部分的面积是:3.14×2²×1/2-(2+2)×2×1/2=2.28平方厘米
难题点拨3想一想做一做
1.(1)13.76平方厘米
(2)31.4平方厘米
(3)1171.5平方厘米
2.(1)57平方厘米
(2)9.42平方厘米
3.628平方厘米
这节课的内容就讲到这里,希望在这节课你能有所收获。下节课我们学习组合图形的面积计算方法。我是小梁老师,下节课见!




