初中数学中考偏难压轴题专项(1)
Jeason_Lan
题号
一、综合题
总分
得分
评卷人
得分
一、综合题
(每空? 分,共? 分)
1、如图1在平面直角坐标系xoy中,已知A(-2,2),B(-2,0),C(0,2),D(2,0)四点,动点M以每秒个单位长度的速度沿B→C→D运动(M不与点B、点D重合),设运动时间为t(秒).
(1)求经过A、C、D三点的抛物线的解析式;
(2)点P在(1)中的抛物线上,当M为BC的中点时,若,求点P的坐标;
(3)当M在CD上运动时,如图2,过点M作MF⊥x轴,垂足为F,ME垂直AB,垂足为E.设矩形MEBF与重叠部分的面积为S,求S与t的函数关系式,并求出S的最大值;
(4)点Q为x轴上一点,直线AQ与直线BC交于点H,与y轴交于点K.是否存在点Q,使得为等腰三角形?若存在,直接写出符合条件的所有Q点的坐标;若不存在,请说明理由.
2、已知抛物线y=ax2+bx+3经过点A(1,0)和点B(-3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为______,抛物线的顶点坐标为______;
(2)如图1,连接OP交BC于点D,当S△CPD:S△BPD=1:2时,请求出点D的坐标;
(3)如图2,点E的坐标为(0,-1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标;
(4)如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.
1/73
3、如图,已知抛物线y=-x2+bx+c与x轴交于A、B两点,AB=4,交y轴于点C,对称轴是直线x=1.
(1)求抛物线的解析式及点C的坐标;
(2)连接BC,E是线段OC上一点,E关于直线x=1的对称点F正好落在BC上,求点F的坐标;
(3)动点M从点O出发,以每秒2个单位长度的速度向点B运动,过M作x轴的垂线交抛物线于点N,交线段BC于点Q.设运动时间为t(t>0)秒.
①若△AOC与△BMN相似,请直接写出t的值;
②△BOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
4、如图,抛物线y=ax2+bx+4交x轴于A(-3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.点P是第一象限内抛物线上的一个动点,点P的横坐标为m.
(1)求此抛物线的表达式;
(2)过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.试探究点P在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标,若不存在,请说明理由;
(3)过点P作PN⊥BC,垂足为点N.请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?
5、如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4,求tan∠BAD的值.
2/73
6、如图,正方形ABCD的边长为2,E为AB的中点,P是BA延长线上的一点,连接PC交AD于点F,AP=FD.
(1)求的值;
(2)如图1,连接EC,在线段EC上取一点M,使EM=EB,连接MF,求证:MF=PF;
(3)如图2,过点E作EN⊥CD于点N,在线段EN上取一点Q,使AQ=AP,连接BQ,BN.将△AQB绕点A旋转,使点Q旋转后的对应点Q"落在边AD上.请判断点B旋转后的对应点B"是否落在线段BN上,并说明理由.
3/73
7、已知二次函数且a=b,若一次函数y=kx+4与二次函数的图像交于点A(2,0).
(1)写出一次函数的解析式,并求出二次函数与x轴交点坐标;
(2)当a>c时,求证:直线y=kx+4与抛物线一定还有另一个异于点A的交点;
(3)当c<a≤c+3,时,求出直线y=kx+4与抛物线一定还有另一个异于点B的坐标;记抛物线顶点为M,抛物线对称轴与直线y=kx+4芙蓉交点为N.设,写出S关于a的函数,并判断S是否有最大值,如果有,求出最大值,如果没有,请说明理由.
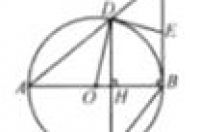
8、如图,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点D,过点D作⊙O的切线与BC交于点E,弦DM与AB垂直,垂足为H.
(1)求证:E为BC的中点;
(2)若⊙O的面积为12π,两个三角形△AHD和△BMH的外接圆面积之比为3,求△DEC的内切圆面积S1和四边形OBED的外接圆面积S2的比.
9、如图所示,在平面直角坐标系Oxy中,等腰△OAB的边OB与反比例函数y=(m>0)的图象相交于点C,其中OB=AB,点A在x轴的正半轴上,点B的坐标为(2,4),过点C作CH⊥x轴于点H.
(1)已知一次函数的图象过点O,B,求该一次函数的表达式;
(2)若点P是线段AB上的一点,满足OC=AP,过点P作PQ⊥x轴于点Q,连结OP,记△OPQ的面积为S△OPQ,设AQ=t,T=OH2﹣S△OPQ
①用t表示T(不需要写出t的取值范围);
②当T取最小值时,求m的值.
10、如图1,△AOB的三个顶点A、O、B分别落在抛物线F1:y=x2+x的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
(1)求点A、B的坐标;
(2)将△AOB绕点O逆时针旋转90°得到△A"OB",抛物线F2:y=ax2+bx+4经过A"、B"两点,已知点M为抛物线F2的对称轴上一定点,且点A"恰好在以OM为直径的圆上,连接OM、A"M,求△OA"M的面积;
(3)如图2,延长OB"交抛物线F2于点C,连接A"C,在坐标轴上是否存在点D,使得以A、O、D为顶点的三角形与△OA"C相似.若存在,请求出点D的坐标;若不存在,请说明理由.
4/73
5/73




