动态问题是初中数学的难点,因为比较抽象,成为许多学生的失分点。动点问题是近几年来各地中考试题中出现的较多的一种题型,它既能考查学生的创造性思维品质,又能体现学生的实际水平和应变能力.其解题策略是“动”中求“静”,“一般”中见“特殊”,抓住要点,逐个击破.
例1
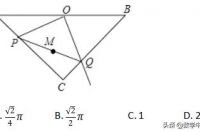
如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( )
【分析】添加辅助线:过点D作DE⊥BC于点E,由图象可知,点F由点A到点D用时为as,△FBC的面积为acm2 . 利用平行四边形的面积求出的DE的长,在Rt△DBE中利用勾股定理求出BE的长,再根据菱形的性质求出EC、DC的长,然后在Rt△DEC中,利用勾股定理求出a的值。
例2
已知:如图,在四边形 ABCD 中, AB∥CD, ACB =90°, AB=10cm, BC=8cm, OD 垂直平分 A C.点 P 从点 B 出发,沿 BA 方向匀速运动,速度为 1cm/s;同时,点 Q 从点 D 出发,沿 DC 方向匀速运动,速度为 1cm/s;当一个点停止运动,另一个点也停止运动.过点 P作 PE⊥AB,交 BC 于点 E,过点 Q 作 QF∥AC,分别交 AD, OD 于点 F, G.连接 OP,EG.设运动时间为 t ( s )(0<t<5) ,解答下列问题:
(1)当t为何值时,点E在 的平分线上?
(2)设四边形 PEGO 的面积为 S(cm2) ,求 S 与 t 的函数关系式;
(3)在运动过程中,是否存在某一时刻 t ,使四边形 PEGO 的面积最大?若存在,求出t 的值;若不存在,请说明理由;
(4)连接 OE, OQ,在运动过程中,是否存在某一时刻 t ,使 OE⊥OQ?若存在,求出t的值;若不存在,请说明理由.
【解析】(1)先分别用含t的代数式表示出线段PE、EC。当点E在∠BAC的平分线上时,根据角平分线的性质可得PE=EC,由此构建方程求解即可; (2)根据S四边形OPEG=S△OEG+S△OPE=S△OEG+(S△OPC+S△PCE-S△OEC)构建函数关系式即可; (3)利用二次函数的性质解决即可; (4)先假设存在。根据余角关系证出∠EOC=∠QOG,则有tan∠EOC=tan∠QOG,即 EC/OC=GQ/OG , 由此构建方程解决即可。




