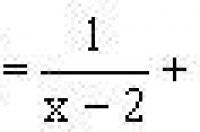
不等式中的均值定理一直是高中数学的重点内容,同时也是高考的重点和热点,也是解决很多问题的重要工具,应用均值定理的前提是满足“一正、二定、三相等”,不过很多时候,题目的条件不满足这一条件,这时就需要适当的“凑”与“配”,下面结合具体例子予以说明。
一、凑“正”
例1. 求
的值域。
解:将
变形为
后可用基本不等式,但不清楚是否为正,因此需要讨论。
由已知得
。
(1)若
,则
,故
,当且仅当
,即
时,取等号。
(2)若
,则
,故
。
∴
,当且仅当
,即
时,取等号。
因此,由(1)、(2)可知
的值域为
。
本题说明“各项为正”这一条件的重要性,当不确定时应进行分类讨论。
二、凑、配“定值”
1. “凑”和为定值
例2. 设一个圆柱的轴截面周长为l,求其侧面积的最大值。
解:设圆柱底面半径为r,高为h,侧面积为S,满足
。
。
当且仅当
,即
时,S有最大值
。
对已知式子进行恰当的“凑”与“配”,再利用基本不等式求最值,这种技巧经常被使用。
2. “配”积为定值
例3. 已知
,
,且
,求
的最小值。
解:∵
,
∴
。
∵
,
,
∴
。
当且仅当
,即
时,取等号。
解得当
,
时,
取得最小值为16。
三、凑“相等”
例4. 求函数
的最小值。
解:
。
设
,则
,此时原式可化为
。
∵
,
∴
。
∴
。
当且仅当
,即
,
时取等号,此时
,解得
。
∴
。
此题是通过加减项的方法配凑成基本不等式的形式,注意换元后
,若对
直接利用均值定理,则需满足
,即
或
,而在
时,无法达到,因此需要凑配“相等”以及积为定值,方可利用均值定理。
▍ 来源:综合网络




