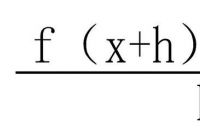
本篇是是上一篇文章
微积分的思维,是对传统方法的降维打击,大道至简其实不难!的延续阅读。
之前,我们已经了解了从微分到积分的转换过程。其实,我们也可以反向推演从积分到微分的转换过程。
对任一可导的函数y=f(x),在区间x∈[a,b]上,有f(b) -f(a),这是曲线y=f(x)在Y轴上的一段投影的长度。
把区间x∈[a,b]分割成无限个无限小,每个无限小记为△x,则有b-a=∞*△x。
那么:
f(b) -f(a)=[f(b) -f(b-△x)]+[f(b-△x) -f(b-2*△x)]+......+[f(a+2△x) -f(a+△x)]+[f(a+△x) -f(a)]
因为△x/△x=1,又得到:
f(b) -f(a)=[f(b) -f(b-△x)]/△x*△x+[f(b-△x) -f(b-2△x)]/△x*△x+......+[f(a+2△x) -f(a+△x)]/△x*△x+[f(a+△x) -f(a)]/△x*△x
=f"(b)△x+f"(b-△x)△x+......+f"(a+2△x)△x+f"(a+△x)△x
因为函数y=f(x)可导,我们把f"(b)~f"(a),记作f"(x),于是得:f(b) -f(a)=∫f"(x)dx,x∈[a,b]。
拿出式中一项,单独表达:[f(x+△x) -f(x)]/△x=f"(x)。因为[f(x+△x) -f(x)]/△x要进行极限运算,表达式记作:
从上述的推演来看,导函数f"(x)是可以由原函数f(x)计算得出的,而原函数f(x)是由导函数f"(x)逆向推导得来的。为了能在微积分计算时,收放自如地推导原函数f(x),我们需要先做好准备工作:求导数f"(x)。
也可以记作:(C)"=0。
也可以记作:(ax)"=a。它也可以视为幂函数y=x^μ当μ=1时的一个特例。
初中学数学的时候,我们先学的幂次方运算后学的指数运算,但求导数不一样,指数函数能用正常的方法求,但幂函数需要借助指数函数的求导结果来求导。所以,我们先来了解指数函数的求导。
也可以记作:(a^x)"=a^x*lna。
当指数函数的底数取自然常数e,也就是a=e时,因为lne=1,所以(e^x)"=e^x。
我们可以先求一个μ为正整数时的特例。取x=a,当x无限趋近于a时,就可以求出y=x^μ在x=a处的导数。
把a替换成x,就有(x^μ)"=μx^(μ-1),把μ从正整数域推广到实数域,这个结论也是成立的。但这是类比推论,(x^μ)"=μx^(μ-1)还需要去证明。这就需要借助指数函数y=e^x和对数函数y=lnx的求导结果以及复合函数的求导方法。我们先把证明贴出来,有需要补对数函数和复合函数求导课的同学,可以回头再来看。
首先我们做一个很有意思的转换:x=e^lnx。有的同学可能忘了对数的运算,那我们先证明一下这个等式。令e^lnx=y,则lnx=lny,x=y,所以x=e^lnx。那么有:
了解了这几个基本函数的导数,反过来求积分,一般的求面积或路程的问题,就不在话下了。