基于Sagnac效应[1]的光纤陀螺用于测量惯性空间的角速度,目前广泛应用于各大领域。其中,捷联惯性导航方面尤为突出,具有无机械活动部件、稳定性好、数字输出精度高、耐恶劣环境等特点。光纤陀螺的输出量容易受到环境因素影响,当工作环境变化时会产生误差,因此,光纤陀螺的温度补偿和误差补偿方法成为研究热点。针对上述问题,通常采用神经网络模型[2]对光纤陀螺误差进行补偿,常用的神经网络有BP神经网络、RBF神经网络、GA-BP神经网络。骞微著等提出建立小波神经网络模型,采用增加动量因子和自适应调整学习速率的方法来改进训练方法,提高了光纤陀螺的输出精度[3];汤霞清等采用小波分析单独重构的方法分离出漂移误差和白噪声,然后对漂移误差数据进行灰化处理,最后使用Elman神经网络对灰化后的漂移误差数据进行建模并补偿,得到高精度的光纤陀螺仪的漂移误差模型[4];顾春雷等利用遗传算法优化网络的权阈值,建立GA-BP神经网络补偿模型[5];杨国梁等采用RBF网络对光纤陀螺进行零漂辨识[6]。本文采用bp神经网络模型,对所有在室温15℃左右的光纤陀螺实验中的所有数据进行建模,并对光纤陀螺输出的光强度进行补偿。为验证本文方法对光纤陀螺误差补偿的有效性,将最终的补偿结果与其他方法进行对比分析;同时,将训练后的网络代入到验证集的数据,验证了本方法的可行性和鲁棒性。bp神经网络算法-
1 光纤陀螺输出信号的处理方法
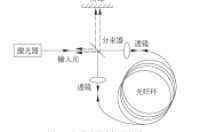
光纤陀螺结构如图1所示,包括激光器,光源,分束器,透镜,光纤环,屏幕等。本次采用的光纤陀螺是根据Sagnac效应为基础开发的实验系统, 激光光源发出的光通过光纤耦合器使两个纤芯之间的光耦合,实现了分光和合光,由于存在角速度,会导致通过光纤环的两束光到达探测器时有不同的延迟,产生相位差,而光强的变化可以反映相位差的大小[7]。利用光电二极管测量光强的变化,通过把干涉光强的变化转换为电信号的变化,得到旋转的角速度。进一步,通过计算机对角速度数据的处理获得零偏、零漂、方差等参数的实时变化。
当光纤环绕垂直于轴心以Ω的角速度旋转时,在两相反方向旋转的光产生的相位差为
(1)
式中,L为光纤长度(可由半波电压和特征频率测得);a为光纤环半径;λ为激光器的波长;c为真空中光速。
当整个系统在光纤环的轴向有旋转时,由于Sagnac效应,输出的干涉光强会发生变化,可以表示为
(2)
式中,I0为初始光强;φs为相位差。
输出光经过光探测器后,通过前置放大器得到输出光强, 并进行A/D转换,利用式(1)、式(2)可得到以SP为单位且与角速度成线性关系的陀螺信号,进而实现对光纤陀螺角速度的实时测量。bp神经网络算法
2 零偏稳定性对光纤陀螺的影响
评价光纤陀螺性能的一个重要指标是陀螺的零偏稳定性, 即陀螺零偏的平均值随平均时间的变化幅度。平均时间短时, 由于白噪声的影响, 会淹没零偏稳定性,出现零偏稳定性变化较大的现象[8]。测试零偏稳定性更好的方法是Allan方差[9]零偏不稳定性,指的是Allan方差曲线在斜率为零时所对应的群平均时间下所计算数据的标准偏差。普遍采用的精度指标有:平滑零偏稳定性σ100s(°)/h(测量时间100s),角随机游走方差测试的零偏不稳定性σBI(°)/h 。它们之间的关系可以近似表示为 有更好零偏不稳定性的光纤陀螺在长期使用测量时会有更小的误差[11]。bp神经网络算法
3 BP神经网络
3.1 模型的建立
在实际测量过程中,陀螺输出量会受到许多因素影响,有较大的非线性,数据处理时会有很大偏差,而 BP 神经网络对非线性函数有较好的处理能力。
BP神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一,它能学习和存贮大量的输入-输出模式间的映射关系,而无需提前给出数学方程。BP 神经网络[12]的结构主要包含输入层、隐藏层和输出层,其中,各层的神经元个数和隐藏层的层数由问题的复杂程度而决定。输出层通常采用线性传递函数[12]。BP神经网络结构如图2所示。
BP算法是一种误差逆传播的算法,学习过程由正反两个反向传播过程组成。进行正向传播时,学习样本通过各层网络依次进行处理,在输出层获得网络的输入响应,如果输出与期望的偏差过大,则将误差反向传输,逐层修正,向减少误差的方向调整,最后到输入层。经多次学习,可以使误差减小到可忽略的范围[13]。bp神经网络算法-
3.2 实验装置
本文选用的光纤陀螺教学系统由光纤陀螺、小型转台、电气控制盒、信号源、示波器和计算机组成[14],其中光纤陀螺固定在转台上,电气控制盒位于地面转台附近,电气控制盒向陀螺提供包括电源在内的所有输入电气信号,并接收陀螺的输出信号。实验仪器型号为GCS-FIGY。
光纤陀螺教学系统的数据采集软件主要完成对陀螺输出数据的采集、显示和保存。软件界面中参数设置区用来设置数据采集参数,主要包括“采样时间”“采样间隔”“通信端口”“平滑数”“标度因数”“Y最大值”“Y最小值”;数据显示区用来显示对软件采集数据的一些统计和计算结果,主要包括“当前值”“最大值”“最小值”“平均值”“方差”“零偏”“零漂”“采样时间”[15]。bp神经网络算法
3.3 误差补偿结果、分析
对BP神经网络进行测试,选12个角速度下的200组数据作为训练样本,进行训练。选取了分布均匀的12个角速度,而舍弃最低最高的极端情况下角速度,角速度分别为0.44、0.47、0.5、0.54、0.59、0.64、0.7、0.78、0.88、1.01、1.18、1.4deg/s。向训练后的神经网络输入600组数据,得到陀螺的平均输出值如图3所示,图中横坐标为实验次数,纵坐标为光纤陀螺输出量的平均值,即在整个采集过程时间内,输出量的平均值。
通过对其补偿前后输出值的分析,得到其补偿前后输出误差的百分比如图4所示,其中误差百分比即每一次补偿后的数值减去补偿前的数值比上补偿后的数值。bp神经网络算法
通过神经网络训练后得到补偿前后的光纤陀螺输出变化曲线,如图3所示,在训练后光纤陀螺的输出平均值随着速度的增加而增加,输出结果与测试结果相一致。通过图4可以直观地看到,经过补偿后,光纤陀螺的输出误差较小。进一步分析,对采用BP神经网络进行训练后,得到的方差与零漂也由较好的改善,如图5和图6所示。
从训练后的曲线可以看出,零漂与方差更加稳定。在训练后,零漂的波动性变得更小,误差也随之减小,在训练后,方差值显著减小,输出更加稳定。通过对数据的进一步分析,如表1所示,可以看出标准差有所减小,相对误差也有大幅减小,进而可以分析得出经过训练后的数据,更加稳定,波动小,显著减小由外界因素产生的偏差。bp神经网络算法
在这个神经网络模型中,输入层有方向、零漂、角速度,输出层为光纤陀螺输出。只要隐藏层的节点足够多,就可以更加精确地逼近函数模型,但是隐藏层的节点个数并没有一种确定的方式得出,所以我们根据资料和经验,在反复验证之后,选择隐藏层节点为8个是最合适的。在神经网络训练完成之后,测试结果达到要求。bp神经网络算法
BP神经网络的优点在于其非线性映射能力,能以更高精度逼近许多非线性函数,且适应能强,容错率高。其缺点在于局部极小化,其往往收敛于不同的局部极小,神经网络算法的收敛速度慢,且其预测与训练能力存在一些矛盾。本光纤陀螺仪输出数据采用BP神经网络具有以下几个优点:首先,使用BP神经网络时,我们可以控制其中一个量进行补偿,不需要同时考虑多个输出量,也可以得到精度很高的输出,为其应用提供便利的条件;其次,准确性好,BP网络补偿精度很高,与其他补偿方法相比,由于其非线性映射能力的优点,可以将精度的量级进行提高。
4 结论
针对光纤陀螺具有复杂非线性、一般补偿方法难以精确补偿的问题。本文提供一种基于BP神经网络的补偿措施,将BP神经网络运用到光纤陀螺误差补偿的工作中,建立了光纤陀螺温度、角速度、标度因数、零漂之间的非线性函数关系模型,使用大量训练样本进行补偿,并对其进行分析。结果有如下几个优点:首先,补偿精度有所提升。通过对训练样本的补偿,得到的数据与原测试数据相比,精度有一定提高。其次,补偿比较便利。使用BP神经网络无需考虑温度对输出及零漂方差等测试量的影响。在光纤陀螺的输出数据时,可以同时得到多个输出量。在通用性方面,BP神经网络的通用性好。在外界条件的影响下,BP神经网络依旧可以以比较高的精度进行误差减小,补偿效果好。最后,神经网络的应用性好。文中对数据训练后的结果与试验结果相比有了很好的补偿,证明了该模型的可应用性。对光纤陀螺的误差补偿有一定的参考价值。bp神经网络算法-