一维搜索
一维搜索就是目标变量只有一个的时候的最优化问题,又称为单变量函数寻优法。
求解这类问题一般有两种方法,一类是区间收缩法(如黄金分割法),一类是函数逼近法(如三点二次插值法、牛顿法)。下面分别介绍:
2:
单谷函数
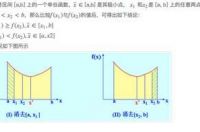
定义:如果函数f(x)在区间[a,b]上只有一个极小值点, 则称f(x)为[a,b]上的单谷函数。
单谷函数具有一个重要的消去性质
3:
外推内插法
在一维搜索中的区间收缩法中需要用到单谷区间,而寻找单谷区间的方法就是下面要介绍的外推内插法
其思路为从某个初始点出发,沿函数值下降的方向前进,直至发现函数值上升为止。而由两边高,中间低的三点,可确定极小点所在的初始区间。
4:
黄金分割法
黄金分割法的思想是:反复使用单谷函数的消去性质,不断缩小包含极小点的搜索区间,直到满足精度为止。
该方法的优点是需计算函数值,通用性强。
5:
三点二次插值法
三点二次插值法的思想是:形式复杂的函数进行数学运算时不方便,因此找一个近似的、解析性能好、便于计算的简单函数来代替,用近似函数的极小点作为原函数极小点的近似,常用于近似的简单函数是二次函数。
因此,最初的三个点x1<x2<x3应构成一个两边高,中间低的极小化框架。
在完成一次计算后,得到近似的x*要进行搜索区间的收缩,然后在新区间中重新构造三点组成的“极小化框架” 。构造的方法为比较f(x*),f(x2),以函数值较小的点为中间点,加上左右两点。
6:
牛顿法
牛顿法是一种函数逼近法,其基本思想是在极小点附近用二阶泰勒多项式近似代替目标函数,求解二阶泰勒多项式的极小点作为目标函数的极小点。牛顿法在数值分析中是用于求解方程的根,而求解函数极值点等价于求其导函数为0时的根(假如函数可微)。