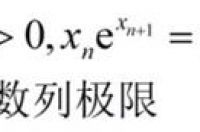
迭代数列的极限问题,可以说是考研数学中的又一个杀手锏
如题
是2018年全国硕士研究生入学考试数学二的第21题
这题是一个典型的迭代数列求极限的问题。
迭代数列求极限一般用单调有界准则证明其收敛,然后方成左右同时取极限来求出极限
首先我们将等式中Xn挪到右边
不难发现,只要第一项大于零,那么后面的每一项都大于零。此结论可用数学归纳法简单证明,此处略去。
接下来证明单调性
直接证明数列Xn的单调性有点不好办,题目中出现的多是Xn的指数韩式形式,不过我们不妨直接证明exp(Xn)的单调性,因为指数函数是单调函数,因而与原数列具有相同的单调性,
由于已经证明Xn>0于是数列的单调性就完全取决于f函数在x>0时的正负
于是讨论f函数
欢迎点赞评论转发




