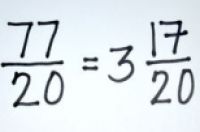
在本文中:将分数化简为最简分数不同分母的分数的加法运算不同分母的分数的加法运算带分数的乘法运算
如果两个分数的值相等,那么两个分数就是等价的。分数1/2和2/4是等价的,因为1除以2的值与2除以4的值是一样的,用十进制形式来表示就是0.5。将分数和带分数转换成等值分数对于分数的加法、减法和乘法运算很有帮助。此外,将分数化为最简分数有利于直观表达分数的值。在做分数加法、减法、乘法运算时,遵循以下的步骤,将等值分数化简(约分)为最简分数。
方法
1:将分数化简为最简分数
1:看看分子是不是大于分母。这样的分数被称为假分数。如果将假分数表示为一个整数加上一个真分数(分子小于分母的分数),这样可能更好理解。而一个整数和一个真分数的组合称为带分数。
如果分子大于分母,那么用分子除以分母。得出来的商就是带分数的整数部分,而余数就是新分数的分子。举例来说,14/8是个假分数,你用14除以8,得到的商是1,余数是6。带分数就是1 6/8(中文读作:一又八分之六),它的值与14/8是相同的。
2:找到分子和分母的最大公因数。最大公因数就是能同时将分子和分母整除的最大数字。以上面给出的带分数6/8为例,分子6和分母8的最大公因数是2。
3:分子和分母分别除以的最大公因数。得到的商将成为新的分子和分母。6除以2的商是3;8除以2的商4。因此,6/8化简(约分)为3/4; 14/8化简为最简分数就是1 3/4(一又四分之三)。
方法
2:不同分母的分数的加法运算
1:找到最小公分母。最小公分母就是所有分母的最小公倍数,也就是能被所有分母整除的最小的数。例如计算11/2 加上2 1/3(二又三分之一)时,最小公分母是6(2 x 3等于6和3 x 2等于6);当计算1/6加上8/9时,最小公分母是18(6 x 3等于18 ;9 x 2等于18)。
找到最小公分母主要是为了让计算简化。在刚才第二个示例中,54是数分母6和9的公倍数。相比于公分母54来说,使用最小公分母“18”可以尽量简化计算,使得算式更为直观,更好去理解。
2:让每个分数的分子和分母分别乘以相同的数,这样可以将各个分数的分母转换最小公分母。也就是说,这可以使每个分数的分母的值都相等。例如计算1 1/2(一又二分之一)加上2 1/3(二又三分之一)时,我们需要将他们的分母都变成6。1/2转化成3/6;1/3转化成2/6。再例如1/6加上8/9,他们的最小公分母是18;1/6转化成3/18;8/9转化成16/18。
3:分子相加。例如11/2加上2 1/3可以转化成1 3/6加上2 2/6,分数部分的和就是(3+2)/6,也就是5/6。再如1/6加上8/9,可以转化为3/18加上16/18,和就是(3+16)/18,也就是 19/18。
4:如果是带分数的话,还需要将整数部分相加起来。例如1 1/2加上2 1/3,1加2等于3,所以整个带分数的和就是3 5/6(三又六分之五)。
5:如果有必要的话,将结果化简为最简分数。如果分子大于分母,那么就用分子除以分母,将得到的商作为带分数的整数部分。例如,1/6加8/9,它的结果用假分数表示为19/18,最终转化成带分数1 1/18。
方法
3:不同分母的分数的加法运算
1:找到最小公分母。
2:让每个分数的分子和分母分别乘以相同的数,这样可以将各个分数的分母转换最小公分母。
3:看看第一个分数的分子(被减数)是否小于第二个分数的分子 (减数)。如果是的话,那就有必要借用带分数的整数部分的值。例如被减数是3 5/8(三又八分之五),减数是1 3/4(一又四分之三);在将减数转换为等值的带分数1 6/8(一又八分之六)后,你会发现,被减数的分子是5,它小于减数的分子6,所以借用整数部分是必要的。被减数的整数部分减掉1,同时分数部分的分子加上与分母一样的值,这样操作之后,新的等值分数就产生了。3 5/8(三又八分之五)就相当于假分数2 13/8(二又八分之十三)。
4:用被减数的分子减去减数的分子。以刚才的例子来说,分数部分的结果应当是(13-6)/8,或者说7/8。
5:如果算式中含有带分数,那还要用‘被减数’的整数部分减去‘减数’的整数部分。由于上例中,借用整数部分的操作是必要的,因此整数部分的结果应该是2-1,或者说是1。所以,被减数减去减数的差应该是1 7/8(一又八分之七)。
6:如果有必要的话,将结果化简为最简分数。
方法
4:带分数的乘法运算
1:将带分数转化成假分数形式。用带分数整数部分的数值乘以分母,然后用得到的积加上分子,这样就得到一个新的分子(也就是假分数的分子)。举例来说,计算2 1/5乘以1 3/4时,你需要将2 1/5转化成(2 x 5 + 1)/5 或11/5;将1 3/4转化成(1 x 4 + 3)/4 或者7/4。
2:分子相乘。在刚刚的例子中,分子相乘就是11 x 7, 或者说77。
3:分母相乘。在刚刚的例子中,分母相称就是5 x 4,或者说 20。所以1 1/5乘以7/4的积就是77/20。
4:如果有必要的话,将结果化简为最简分数。如果结果是个假分数,那么你需要将它转化成带分数,并且分数部分应当化简为最简分数(分子和分母的最大公因数是1) 在刚刚的例子中,假分数77/20应当转化为带分数3 17/20(三又二十分之十七)。
小提示
将分数转换为等值形式,实际上就是原分数乘以1。例如将1/2转化为 2/4,就是分子和分母同时乘以2 ,也就是1/2乘以2/2,2/2的值就是1。
警告
分子和分母同时乘上一个数时,原分数的数值不变,但如果是分子和分母同时加上一个数的话,原分数的数值可能与新分数的数值不同。所以,转化等值分数时,你千万不要使用后面那种方法。




