受疫情影响,到现在孩子们还没进行系统的学习,若中考不延期的话 ,离中考还有不到100天,为了帮助初三的孩子们,民哥特做一些专题复习,当然专题内容不会特别难,都是指向当前考试.
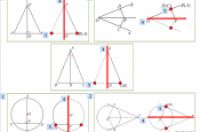
今天我讲的主题是几何图形三大变化之翻折,那么我们首先来看一看初中阶段常见的几何翻折基础图形.
上面几副图是我们初中阶段常见的翻折图形,那么翻折图形具有什么性质特点呢?我们来看一看:
1.翻折前后两部分图形形状相同、大小不变,关于折痕成轴对称;
3.翻折得到轴对称图形、线段垂直平分线、线段相等、 角的平分线.
其实归根结底,翻折的本质就是轴对称.
好了,接下来,我们看几道宜宾最近几年期末或中考试题.
分析,由图形的翻折可以知道角APO=角B=90°,又因为角D=90°=角C,故有一线三等角证明相似,具体过程如下:
通过上面我们可以看图形的翻折得到图形的对应角相等,故平时积累的基础知识是解题的关键,同样我们知道翻折的对应线段相等,故知道PO=BO,从而找到PO和CO的关系,故容易求,具体过程如下:
我们接下来看一道2015年宜宾中考试题,这个题当时得分率并不高,那么若我们掌握了基本性质后会发现非常简单,我们先呈现原题:
我们看这里题中给出了C点,而它的对应点是点O,故可连结OC,得到AB垂直平分OC,也能得到OC的函数解析式,故可以轻易搞定,具体过程如下:
当然这道题解法很多,比如抓住翻折图形的对应线段对应角相等,可由勾股定理得道AC,即得到OA,再由角度关系求出OB,自然可求AB的函数解析式,过程如下:
而由翻折知道角相等,自然有角ACB是直角,有直角就可以构造一线三直角,故有解法三.,具体过程如下:
我们接下来,继续思考一道宜宾市最近的中考题,即2018年宜宾中考16题,依然考察的翻折,我们先看原题:
我们看第一个问题,当E为AB中点时,AF平行CE,其实只要抓住翻折图形对应线段相等,利用等腰三角形导角即可证明,具体过程如下:
我们再看第二个,同等条件下求AF的长,其实题中告诉了AB、BC的长,自可求出CE的长,可求出角1的余弦,从而求出角4的余弦,故可求,具体过程如下:
我们继续看第三问,说A、F、C三点共线,由翻折很容易得到CF,由勾股定理又很容易得到AC,故容易求出AF和角BAC的余弦故可求出,具体过程如下:
由题意很容易知道AE不等于CE,故第四是错误的.
我们上面分析的三个题,在宜宾的期末考试或中考来说都是拉分的,但我们可以看,只要我们真正的掌握了基础知识,中考高分并不难.最后我们总结一下翻折图形解题的策略:




