中考动点最值一直是个难点,本题大家通常说是瓜豆原理,也说是主从联动,我个人理解本题的构造两个方向,一种是等腰直角三角形“脚拉脚”模型出相似,另一种是等腰直角三角形“手拉手”模型造全等。我们先看下题目:(以下题目不是我的,过程和方法及图是自己做的)
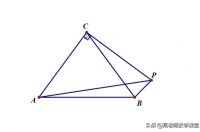
平面内两定点A、B之间的距离为8,P为一动点,且PB=2,连接AP,并且AP为斜边在AP的上方作等腰直角三角形APC",如图,连接BC,则BC的最大值与最小值的差为 ( ).
我们先看下构造方法:前4种是“脚拉脚”相似构造,后2种是“手拉手”全等构造
思路一:
构造等腰直角三角形“脚拉脚”模型
△ACE∽△APB(相似比1:√(2))
∴CE=√(2),BE=4√(2)
∵BE-CE≤BC≤BE+CE
∵2CE=2√(2)
∴BC的最大值与最小值的差是2√(2)
思路二:
构造等腰直角三角形“脚拉脚”模型
△ACB∽△APD(相似比1:√(2))
∴PD=√(2)BC
∵BD-BP≤PD≤BD+BP
∵2BP=4
∴PD的最大值与最小值的差是4
∴BC的最大值与最小值的差是2√(2)
思路三:
构造等腰直角三角形“脚拉脚”模型
△DCP∽△BAP(相似比1:√(2))
∴DB=√(2),CD=4√(2)
∵CD-BD≤BC≤CD+BD
∵2BD=2√(2)
∴BC的最大值与最小值的差是2√(2)
思路四:
构造等腰直角三角形“脚拉脚”模型
△BPC∽△DPA(相似比1:√(2))
∴AD=√(2)BC
∵AB-BD≤AD≤AB+BD
∵2BD=4
∴BC的最大值与最小值的差是2√(2)
思路五:
构造等腰直角三角形“手拉手”模型
△ABC≌△PDC
∴AB=PD=8,BD=√(2)BC
∵BD-BP≤BD≤BD+BP
∵2BP=4
∴BC的最大值与最小值的差是2√(2)
思路六:
构造等腰直角三角形“手拉手”模型
△ADC≌△PBC
∴AD=PB=2,BD=√(2)BC
∵AB-AD≤BD≤AB+AD
∵2AD=4
∴BC的最大值与最小值的差是2√(2)
通过本题6种构造方法,你是否真的掌握了?我们一起做一下练习,孰能生巧。以下两道题作为练习,方法不唯一,有兴趣的研究下:
1.如图,在直角三角形ABC中,∠C=90°,D是AC边上一点,以BD为边,在BD上方作等腰直角三角形BDE,使得∠BDE=90°,连接AE,若BC=4,AC=5,则AE的最小值是( ) .
解:以AD为直角边,点D为直角顶点作等腰直角三角形ADF
连接BF.
易证△AED≌△FBD
∴AE=BF
∵∠FAD=45°
∴点F在AF方向运动,∠FAC=45°
∴点B到射线AF的距离最小
∵AC=5,BC=4
∴AE的最小值为(√(2)/2)
2.如图,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4√(2),对角线BD⊥CD于点D,求对角线AC的最大值( )
思路:构造等边三角形手拉手造全等即可,AC≤2√(6)+√(2)
中考最值问题视频专栏:
免费圈子:




