一、费马点的由来
费马(Pierre de Fermat,1601—1665)是法国数学家、物理学家.费马一生从未受过专门的数学教育,数学研究也不过是业余爱好. 然而,在17世纪的法国还找不到哪位数学家可以与之匹敌.他是解析几何的发明者之一;概率论的主要创始人;以及独承17世纪数论天地的人. 一代数学大师费马堪称是17世纪法国最伟大的数学家. 尤其他提出的费马大定理更是困惑了世间智者358年.费马曾提出关于三角形的一个有趣问题:在△ABC内求一点P,使 PA+PB+PC之值为最小,人们称这个点为“费马点”.
二、探索费马点
1. 当三角形有一个内角大于或等于120°的时候,则费马点就是这个内角的顶点.
下面来验证这个结论: 如图1,对三角形内任意一点P,延长BA至点C′,使得AC′=AC, 作∠C′AP′=∠CAP,并且使得AP′=AP. 即把△APC以A为中心做旋转变换. 则△APC≌△AP′C′,
∵∠BAC≥120°,∴∠PAP′≤60°. ∴在等腰三角形PAP′中,AP≥PP′,
∴PA+PB+PC≥PP′+PB+ P′C′>BC′=AB+AC. 所以A是费马点.
2. 如果三个内角都在120°以内,那么,费马点就是三角形内与三角形三顶点的连线两两夹角为 120°的点.
如图2,以B点为中心,将△APB旋转60°到△A′BP′. 因为旋转60°,且PB=P′B,所以△P′PB为正三角形. 因此,PA+PB+PC=P′A′+P′P+PC.
由此可知当A′,P′,P,C四点共线时,PA+PB+PC=P′A′+P′P+PC为最小.
当A′,P′,P共线时,∵∠BP′P=60°,∴∠A′P′B=∠APB=120°. 同理,若P′,P,C共线时,则∵∠BPP′=60°, ∴∠BPC=120°.
所以点P为满足∠APB=∠BPC=∠CPA=120°的点.
二、费马点相关问题
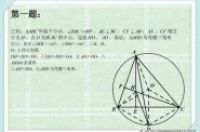
等腰直角三角形,已知在直角平分线上的一点P,PA+PB+PC最小值为√6+√2,求直角边的长度?
解答:如图
将三角形PAC逆时针旋转60度得三角形DEC,则角PCD=60度,三角形PCD是正三角形,PC=PD且DE=PA,所以PA+PB+PC=DE+PD+PB,根据两点之间线段最短,当点E、D、P、B在一条直线上时,DE+PD+PB最小,这时∠BPC=120°,∠APC=∠EDC=120°
下证这时的点P就在角ACB的平分线上。
在三角形DCE和PCB中,因CE=CA=CB得角E=角PBC,又有∠EDC=∠BPC=120°,
得三角形CDE、CPA、CBP全等,∠ECD=∠ACP=∠BCP,点P在∠ACB的平分线上。
所以点P是这样一个点:它使∠APC=∠BPC=∠APB=120度(这个点叫三角形的费马点)。
延长CP交AB于F,则CF垂直AB,且由三角形CPA、CBP全等知PA=PB,得角FPA=60度,
设PF=x,则PA=PB=2x ,AF=CF=√3*x,PC=(√3-1)x,有 2x+2x+(√3-1)x=√6+√2,x=1/3√6。所以 AF=CF=√2,AC=√2*CF=√2*√2=2。
三、费马点与中考试题