高中几何蝴蝶定理专项练习

　　蝴蝶定理

　　例一

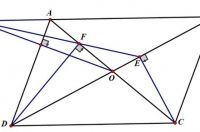
　　1、已知：如图，O为平行四边形ABCD中心，DF⊥AC于F,CE⊥BD于E,EF交AB于G。

　　求证：GO⊥AD

　　（高中联赛难度几何100题之74，田开斌题）

　　思路分析：显然CDEF共圆，圆心J为CD中点，从而需证GO⊥JO，这显然是蝴蝶定理之逆，延长GO交DC于K，则OG=OK,从而得证

　　证明：设GO交CD于K，由对称性知OG=OK；

　　设J为CD中点，由垂直得CDFE共圆，且圆心J为BC中点，

　　由蝴蝶定理逆定理即知JO⊥OG，

　　又由中位线定理得OJ//AD,

　　故GO⊥AD。

　　注：本题证明方法比较多。除了上述蝴蝶定理方法以外，还可以用根轴（田开斌老师的解答就是利用根轴解决的）。当然还可以使用其他计算方法等。不过如果能想到蝴蝶定理，本题能迅速得到解决。

　　例二

　　已知：如图，△ABC中，D为BC中点，以AD为直径的圆交AB、AC于E、F。

　　此圆在E、F处切线交于G。

　　求证：GD⊥BC

　　思路分析1：类似蝴蝶定理证法2，过G作两边垂线，由垂直得共圆倒角得相似，为了利用垂直，采用同一法。

　　证明1：根据图形的唯一性，我们证明其逆命题，即由GD⊥BC证明BD=CD,

　　设GH⊥AB于H,GI⊥AC于I,

　　由切线知∠HEG=∠EDA,∠IFG=∠FDA,

　　又GE=GF,故HF:ED=GE:AD=GF:AD=IF:DF,

　　故∠EDH=∠FDI。

　　由垂直得BHDG,GICD共圆，又GH//DE,GI//DF,

　　则∠DBG=∠GHD=∠HDE=∠FDI=∠DIG=∠DCG,

　　故GB=GC,DB=DC，证毕。

　　思路分析2：看到平分和垂直想到蝴蝶定理。

　　E、F在以G为圆心的圆上，由切线倒角得到IGJ共线，

　　由垂直得直径与共圆，

　　利用蝴蝶定理逆定理即得。

　　证明2：如图，显然GE=GF，

　　设以G为圆心GE为半径的圆交射线AB、AC于I、J，

　　由GE为圆的切线得∠EIG=∠IEG=∠AFE=∠EIJ,

　　故IGJ共线。

　　又∠AED=90°,则E,D,J共线，

　　同理F,D,I共线。

　　又DB=DC,

　　由蝴蝶定理逆定理知GD⊥BC。

　　注：1）证法1相当于证明了本题的逆命题，本题的证明严格上可以这样叙述：

　　设过E的圆的切线交过D的BC的垂线于G",G"F"为圆的另一个切线，

　　AF"交BD于C",由证法1知DB=DC",从而C,C"重合，即原结论成立。

　　2）证法2将其巧妙转化为蝴蝶定理，不过还要由切线证明三点共线，才能完成证明。本证法最终图形与《蝴蝶定理之八》的第1题殊途同归。将其对照会有更多收获。这也算是本题的一种本质。

　　3）本题有很多解法，叶中豪老师得到不少解法，也对其做过很多推广。不过一言以蔽之：蝴蝶定理算是本题的一种本质认识。

　　例三

　　如图，已知△ABC旁切圆I切三边于D,E,F,EF交ID于H，AH交BC于M。

　　求证：MB=MC,

　　（1991年四川省竞赛题）

　　思路分析1：类似于切割线蝴蝶定理证法1，过H作BC平行线，得到共圆倒角即可。

　　证明1：设过H的BC平行线交AB,AC于J,K，

　　由垂直得IJFH,IHKE共圆，

　　故∠IJH=∠IFH=∠IEH=∠IKH,

　　故IJ=IK,HJ=HK,

　　由JK//BC,从而MB=MC。

　　思路2：利用正弦定理或分角定理以FH:HE为媒介进行计算即可。

　　证明2：设△ABC三个角为A,B,C,

　　由垂直得BFID,DIEC共圆，

　　故∠FID=∠B,∠DIE=∠C,

　　△IFE中，由正弦定理得：

　　FH:HE=sin∠FID:sin∠DIE=sinB:sinC,

　　△AFE中，由正弦定理得：

　　sinB:sinC=FH:HE=sin∠FAH:sin∠HAE,

　　△ABC中，由正弦定理得：

　　BM:CM=ABsin∠FAH:(ACsin∠HAE)

　　=(sinC:sinB)*(sin∠FAH:sin∠HAE)=1,

　　即MB=MC。

　　注：1）解法1通过精妙的平移转化，轻松倒角得证。其思路和《蝴蝶定理之四》第1题的最经典的证法1异曲同工。也与上题的思路1如出一辙。

　　2）证法2没有添加辅助线，只是通过简单三角计算即得，也不失为一种合理的证法，值得体会学习。

　　3）本题很经典，解法也很巧妙简洁，人见人爱，花见花开。我们在鸡爪定理里面反复强调，每一个内心具有的性质旁心都有。不难想象，本结论对内切圆也是成立的，这正是2010年北方竞赛的第6题，如下图所示。证明当然也是如出一辙。

　　例4、已知：如图，△ABC中，D、K分别为BC、AD中点，E、F为D

　　AB、AC上垂足，

　　KE,KF交BC于M,N。O、O"为△EMD、△FND外心。

　　求证：OO"//BC

　　（2017年东南数学奥林匹克竞赛第2题）

　　思路分析：设圆O、O"交于D、G。若OO"//BC则GD⊥BC,GE⊥ME,GF⊥FN,则本题

　　化为第2题，下面只需考虑如何转化即可。想到第2题证法2，利用其辅助线及蝴蝶定理即可证明。

　　证明：如图，设DE交AF于L，DF交AE于J，LJ中点为G，

　　由垂直得JEFL、AEDF共圆，

　　则∠GEJ=∠GJE=∠AFE=∠ADE=∠KED

　　则GE⊥KE,同理GF⊥KF。

　　由DB=DC,根据蝴蝶定理逆定理知GD⊥BC。

　　故MEDG,NFDG共圆，

　　故O、O"为MG、NG中点，

　　则OO"//BC

　　注：本题证法比较多，上述证法是本人联系到第2题得到的。这也说明本题的本质是蝴蝶定理，算是第2题的进一步加深。