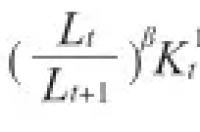
一、引言
资本积累对推动经济增长的重要性,从来没有在古典经济学、现代经济增长理论、新古典增长理论、及当前广受国内外学者关注的干中学模型等所有经济理论中缺席。中国改革开放三十余年来,资本积累对经济增长的贡献更受到了广大学者的关注。王小鲁等指出,1999—2007年间,资本投入对经济增长的拉动作用为3.8%;邱晓华等利用1980—2004年的数据对中国经济增长的贡献率进行了分解,认为资本投入对经济增长的拉动作用为5.8%,但是对经济增长的贡献率高达59.2%,其间中国的资本形成率超过了40%。蔡昉对中国1978—1998年的经济增长进行分解后,认为物质资本增长对其贡献份额达到28%。资本投资高速增长的红利效果必然不会永远持续下去,对其未来的结束时间和经济状态的预测和评估对把握经济发展节奏具有重要的意义。
当前关于资本投资对经济增长贡献研究中最重要的理论依据是边际报酬递减规律:随着投资总量的增加,单位投资获得的回报率将会逐渐降低直至为零。届时,理论上将不再有多余的新增资本投资,从而资本投资增加对经济增长的推动作用将会结束。现有的大量研究都是围绕这个理论展开的,试图回答中国资本投资回报率或者效率目前的水平是多少,具有怎样的发展趋势等问题,但由于研究角度不同、方法不同、数据样本不同等很多原因使得结果并不一致:(1)中国的资本投资回报率相对稳定。孙文凯等通过对中、美、日2006年以前的投资回报率进行估算认为,资本回报率受经济周期影响,长期资本回报率遵从一个递减的趋势;黄先海等从资本深化和技术进步的视角对中国资本回报率变动的原因进行了分析,都得出“中国的资本回报率并没有随投资的增长而降低,资本深化虽然导致了资本回报率的降低,且乘数放大了这种效应,但技术进步却提高了资本的边际产出,从而使得中国的资本回报率处于一个稳定水平”的结论。(2)中国的资本投资回报率较低或开始下降。辛清泉等通过对上市公司1999—2004年的资本回报率进行估算,得出中国上市公司的投资回报率较低的结果,并对该现象进行了投资环境等原因的分析;张勋和徐建国用两种方法对中国资本回报率进行了测算,认为中国总体资本回报率从1998年开始持续上升,到2009年出现下降,但工业资本回报率依然呈现上升态势等结论;白重恩和张琼利用面板数据对1978—2012年中国全国和各省的资本投资回报率进行了估算,发现资本回报率呈现出非常明显的惯性特征,随着时间的推移而不断下降;投资率对资本回报率存在统计显著的负向影响,而第二产业和第三产业比重对资本回报率有显著的正向影响。(3)中国的资本投资回报率是上升的。方文全从年份资本理论视角讨论投资、折旧和资本积累的基础上重估了中国1993—2007年的资本回报率,结果发现资本回报率的长期趋势由投资来源及其增长模式所决定,而资本回报率回升的重要原因是要素效率提高导致的资本份额上升;陈培钦对“中国奇迹”从资本回报率、生产率等角度给出了解释,利用干中学模型和面板数据模型进行研究,认为中国生产率增长和资本回报率增长之间是良性互动的,成就了中国的高速发展;刘晓光和卢峰利用扩展的二元经济模型,发现劳动力转移与技术溢出效应结合是导致中国资本回报率上升的重要原因;龚六堂和谢丹阳利用省份数据从中国资本的边际生产率角度展开研究,得出了中国大多数省份资本存量的边际生产率的差异在1970—1993年之间是下降的,而1993年之后却是上升的结论。
上述研究结果的不一致性表明,从边际报酬角度看中国当前资本投资对经济增长发挥作用程度的相关研究结论并没有达成共识,而且这些研究多集中在对资本投资回报率的估算和趋势的讨论上,对于中国将会在什么样的情况或时间节点下,资本总投资达到不再增加的临界点这样的问题则更难回答。既然投资有回报是资本积累的动力,反之资本停止积累的原因是否只是投资不再具有回报率?是否存在其他原因导致资本积累无法继续增加、进而无法继续促进经济增长?本文希望避开关注资本投资回报率变化这样间接且不易得到一致结论形式的讨论,直接考察在现有生产水平和其他影响条件不变的前提下,通过资本积累特征和路径规律的角度,讨论固定资本存量停止积累的条件和估算停止积累时中国可积累固定资本存量的最大值及对应的最大产出。并进一步预测资本投资积累红利能够推动中国经济以新常态速度持续增长的时间。
文章将从理论分析、模型证明和实证估算角度,依固定资本存量积累的路径解析最大固定资本存量存在的理由和影响条件,预估资本红利未来持续对中国经济增长的贡献。全文共分四部分:第一部分,问题的提出以及现有相关研究的梳理;第二部分,对影响资本积累的原因进行理论分析,并利用永续存盘法和C-D生产函数模型从资本积累路径角度对可积累的最大固定资本存量进行推导;第三部分,利用1986—2013年数据对中国经济进行实证检验,并估算中国可积累的最大固定资本存量;第四部分,结论与建议。
二、理论及数理分析
从投入要素角度看,中国经济长期高速增长的动因主要是劳动力红利、技术进步和资本投资的增加。其中技术进步是被公认的唯一可持续发展的主要动力因素,中国正在进行的经济增长方式转换性改革就是为了实现未来技术进步作为中国经济以较高速度可持续增长的最重要动力形式。劳动力红利可持续支持中国经济发展潜力的问题已有较全面的研究结果。资本投资作为经济增长的主要动力因素之一,同样受到了人们大量的关注。现有研究更多强调了其注重利益的一面,也就是只要投资回报率大于0,从投资角度看有利可图,资本就会不断获得积累和增加。但现有的大量关于中国资本回报率的研究结果并不一致,甚至相互矛盾。这使得关于中国资本红利将何时结束的问题很难得到回答。那么跳出投资回报率的因素,从资本积累增加对经济增长贡献的本质和其本身积累的规律特征角度是否可以获得关于固定资本积累停止增加的信号?
(一)资本投资对经济增长贡献的理论分析
资本投资对中国经济增长的作用可以体现在间接和直接贡献两个方面。从间接贡献角度看,二元经济的发展和剩余劳动力的顺利转移离不开资本投资的增加。中国的二元经济增长现象作为一个单独的发展阶段体现在新古典经济状态之前。而二元经济存在的根本原因是传统经济部门的剩余劳动力和经济体的贫穷造成的。正是对富裕、美好生活的向往使得人们积累资本、创新科技以增加生产,从而现代经济部门得到扩张和发展。传统经济部门剩余劳动力的规模和投资与现代经济部门的资本额度等因素共同决定了二元经济社会的发展速度和持续时间。传统部门剩余劳动力存在与否等现象决定了二元经济是否存在,而现代部门的资本投资规模以及劳动力报酬等因素决定了现代经济部门能够吸收剩余劳动力的数量和速度。因此,没有投资资本的积累,就不能保证传统部门剩余劳动力的转移,也就不能推动二元经济的发展。从资本投资对经济增长直接贡献的角度看,在以规模报酬不变的C-D生产函数表现的现有生产力水平下,由于产出是投入要素的幂函数,其他因素不变时,只要投入要素持续增长,产出就能够保持增长状态。虽然中国当前劳动力总量在一段时间内增加的可能性不大,但只要固定资本投资总量是增长的,经济增长就能够持续。
既然只要资本投资能够增加,其对经济增长的促进作用就不会停止。那么,接下来很重要的问题就是资本投资的增长何时停止?资本存量指在一定时点上所积存的实物资本总量,由于物品的耐用性不会立即消失,资本是可以以一定的折旧率积累到下一期的。因此,资本存量的计算通常包括前期资本折旧后的剩余加上当期的新增投资。从而,新一期的资本存量受前期资本存量、折旧率和新增投资的影响。以被考察经济体积累初期资本存量的高低可把其分成两类:第一类,是初期资本存量较低的经济体(这是很多国家发展开始时的状态)。如果该经济体的折旧率相对较低,而新增投资较高,在弥补前期折旧的基础上仍能保证资本的增加,则其资本存量能够得到快速的积累和提高。这使得资本红利对经济增长有很大的促进作用(中国的经济发展无疑具有这种特征)。资本的快速积累和经济的持续发展会把该经济体转变为下面将讨论的第二种类型。反之,如果该经济体的折旧率不低,同时新增投资又不高,则新增投资只能(甚至不能)弥补前期折旧,经济体的资本存量就只能得到很慢的增长(甚至不能够得到增长),从而资本投资对经济增长的促进作用很低(或者没有)。世界上一些经济长期得不到发展的国家资本存量的变化接近这种情况。另一类经济体是,被考察的初期资本存量就很高(世界上的发达国家目前的状态),即使仍能保持较低的折旧率,但相对较高的折旧资产需要更高的新增投资来弥补,因此,在假设包括生产水平在内的其他因素都没有变化的前提下,资本存量积累的理想的状态是每期资本的新增投资正好弥补资产折旧,从而使固定资本存量维持在一个相对稳定的状态。如前面所提,当资本处于积累增加的路径上时,必有新增投资的增加大于前期资本折旧的数量。随着资本累积总量的不断增加(十倍或者更多倍于产出水平),需要更多的新增投资对逐渐增加的折旧进行补充。而其他因素不变时,受生产方投入要素边际报酬递减规律影响的产出增加幅度却逐渐放缓,从而按照产出固定比例获取的新增投资必然增长更加缓慢。两者相向而行必将相遇。当新增资本投资恰好补充前期资本折旧的损失时,经济体将进入相对稳定状态。只有相关影响因素发生改变时,才会打破这种稳定,但固定资本存量会在所有影响因素都相对稳定之后再次进入稳定状态。因此,固定资本存量积累到一定水平后的理想状态是维持稳定。本文后面将结合数理公式证明该结论。
事实表明,现实中的实物资本折旧率都可以较低。中国现有的研究中常用的折旧率多在5%左右,也有研究者认为在3%附近,或者在10%左右的。受到确定的折旧率、投资率和要素规模报酬递减的投入产出关系等因素影响的固定资本存量不会永无止境地增长下去,其对经济增长的红利作用也会因资本存量不再增加而停止。那么,在一定的经济发展条件和确定的生产力水平下,任何经济体都应有一个可积累的最大固定资本存量值。(这里所说的一定的经济发展条件包括新增固定资本投资满足一定的规律,折旧率确定不变和劳动力总量不变等。)届时,如果新增资本投资能够抵消折旧,则资本存量将处于该最大固定资本积累值处不变,这个资本存量值也就是西方经济学理论下的稳态资本水平。当生产条件以一定的规律发生改变时,资本存量的最大值也可以随着这规律改变,这也就是资本的动态稳定水平。由于以美国为首的西方经济发达国家早早进入了劳动力和资本要素的稳态状态,仅依赖技术进步等全要素生产率为主的动力因素的提高促进经济增长,导致西方经济学对资本朝稳态水平积累过程中的经济体特征研究、讨论较少。中国与其相反,目前仍处在朝稳态最大固定资本存量积累的过程中。因此,我们应该更关心(动态)最大固定资本存量的积累路径和影响因素。相应地,对于中国当前的经济现状,在其他条件不变时,可积累的最大固定资本存量将是多少,与其对应的最大产出会是多少,这个资本红利还能够推动中国经济以新常态速度发展多长时间都是本文希望回答的问题。这对保证人们生活水平稳步上升前提下把握中国当前经济增长方式转换和经济体制转型的节奏,顺利度过改革过渡期具有重要的理论和现实意义。
全文证明与实证研究都将基于规模报酬不变的C-D生产函数模型进行,见如下公式:
Y=AKαLβ=AK1-βLβ (1)
其中,0<а,β<1,且α+β=1。
不失一般性,假设代表技术进步的效率参数是时间的函数,和资本积累无关,资本存量以及劳动力数量也都只是时间的函数。则随时间变化的C-D生产函数一般化模型形式如下:
Yt = AtKtαLtβ= AtLtβKt1-β (2)
(2)式说明,产出是固定资本投资的增函数,虽然资本的边际产出会下降但不会低于零。对固定资本存量,本文使用永续存盘法计算,公式如下:
Kt=(1-t)Kt-1+I t (3)
其中,δt为固定资产折旧率,It为当期新增资产投资数量,受前期产出的约束。固定资本存量的计算公式说明,如果新增资本投资的数量不能抵消前期资本存量折旧所带来的损失,则资本投资将不会有正向的增加,从而其他条件不变时不能引起相应产出的增加。对于新增资本投资增量It ,本文假设其是外生变量,是前期产出的比例,该比例可以随时间变化,记成:
It = ctYt-1 (4)
ct的取值在0—1之间。经济正向增长的基本表现是下一期的产出高于当期产出,则应有:
At+1Lβt+1K1-βt+1 =Yt+1≥Yt = AtLtKt1- β (5)
整理(5)式可得:
设 rt = A t/A t+1,lt=L t/Lt+1。经济正常发展时,在技术进步的保证下,生产效率系数不会下降,有At+1≥rt At,因此,有0<rt ≤1。但是,lt和1的大小关系不能确定,当一国的人口和劳动力数量处于增长时期时,lt≤1,当一国进入老龄化社会、劳动力的数量开始下降时,就会发生lt≥1的情况。把公式(4)、(5)和生产函数Yt = AtKtαLtβ分别代入不等式(6)的左侧,则有:
[(1-δ )Kt+ct At LtβKt1-β]1-β ≥ rt ltβKt1-β (7)
整理得:
[1-δ +ct At LtβKt1-β]1-β Kt1-β≥ rt ltβKt1-β (8)
从而:
[1-δ +ct At LtβKt1-β]1-β ≥ rt lt (9)
1-δ +ct At Ltβ/Ktβ ≥ (rt ltβ)1/1-β (10)
根据模型设定时参数的取值范围有0<1-β <1,则上述不等式有意义,进一步整理出:
最后:
如此,本文从数理推导角度证明了当生产条件不变时,能够促进经济增长的固定资本存量存在动态条件最大值。该动态条件最大值受很多相关因素的影响,并且当影响因素随时间的变化而发生变化时,可积累的固定资本存量最大值也会发生变化。具体看可积累的固定资本存量最大值与生产效率参数和劳动力数量有正相关关系,同时与当期投资占前期产出的比率有正相关关系,同前期与当期劳动力比值和前期与当期生产效率系数比值分别具有负相关关系,与固定资本存量的折旧率和劳动要素弹性系数有负相关关系。值得强调的是,可积累的最大资本存量与劳动要素弹性参数之间的负相关关系表明,如果增加劳动力弹性参数,会使可积累的最大固定资本存量极值降低,从而影响相应的最大产出和经济增长效果。反之,减小劳动弹性系数能增加可积累的最大固定资本存量极值,从而增加最大产出,扩大经济增长效果。
三、实证检验与预测
(一)数据选取和计算
样本数据的使用和选取方面,根据生产函数的形式分别需要中国经济总体的总产出、劳动力投入量和固定资本存量数据。其中固定资本存量数据由于没有官方的统一公布,需要利用现有指标进行估算。现有的多种算法中理论、方法和结论并不唯一,获取权威结果相对困难。虽然关于固定资本存量数据的计算理论和方法的选择等问题作者也有自己的观点和看法,但鉴于其不是本文的研究目的,不在此处进行详细论述。根据数据的可得性、准确性和可比性以及作者的分析与筛选,本文借鉴李仁君关于固定资本存量的数据和计算方法。李仁君给出的是1986—2007年的数据,本文将研究的时间扩展到2013年,后几年的投资数据由《中国统计年鉴》获得,进行处理后,很容易在其方法基础上获得接下来各年的资本投资总量数据。由于1986年之前的中国经济与本文所考察之当前状态相距较远,本文不再对其数据进行收集和取样。关于劳动力数量和产出的相关数据皆从《中国统计年鉴》获得。所有数据以1986年为基期进行可比性修正。为了进行下文的分析,表1中列出了中国经济总体进行可比性处理后的历年相关数据。
(二)在当前生产力水平下中国最大资本存量的估算和相关节点预测
不等式(12)的获得假设了代表生产效率的系数A、新增投资以及劳动力数量都可以是变的,具有相对一般性。根据中国经济的现状和本文的研究目的,为了估计当前情况下固定资本存量的最大值,本文继续假设未来中国的劳动力总量将维持当前的水平不变,这也较符合中国当前的经济状况;假设生产函数的效率系数没有变化,也就是系数A为常数;以及假设新增投资占前期产出的比率确定,这也是目前国际上公认的一个现象。不同国家具有不同的投资、消费习惯。美国投资占产出的比例较低,一般在15%左右,而中国人由于储蓄率较高,投资占产出的比例也较高。则不等式(12)可简化为:
根据(13)式,对满足假设条件的最大固定资本存量的估算,还需要关于当前生产函数的资本或劳动力的产出弹性参数和全要素生产率参数、固定资本存量的折旧率、当期投资占前期产出比例参数以及当前劳动力数量的估算。这些都和当前的生产能力以及经济现状有关。
为了充分体现中国当前经济现状,在进行了各种形式估算后,本文选择使用2001—2013年作为代表中国当前生产能力(考察中国当前生产函数形式)的样本空间,把基于这个样本估计得到的生产函数作为中国当前生产能力对应的生产函数。继续应用固定资本存量折旧率为=5%,应用同样样本空间数据估算出当期资本投资占前期产出的比例,未来假设劳动力总量不变,使用2013年中国劳动力总量的数据L=76977万人,应用公式(13)和对应的生产函数推导出可积累的最大固定资本存量和相应最大产出。数据及结果见表2。
表2给出了基于2001—2013年的样本数据所估算出的中国当前经济C-D生产函数中全要素生产率A=0.346、劳动要素弹性系数=0.528,这个时期投资占前期产出比例的平均值为59.4%,同时结合折旧率以及中国未来劳动力总量维持2013年水平不变的假设,得到能保持中国经济持续增长的可积累最大固定资本存量以1986年价格水平计算约为1119531.31亿元。再次利用生产函数计算其他因素不变条件下,固定资本存量达到最大值时,中国能获得最大产出约为1986年价格水平时的94236.64亿元。根据中国2013年的产出数据看出,这个最大产出值约为中国2013年产出的2倍,当前还远未达到该最大产出水平。该最大产出折算成2013年的价格水平时约为1170582亿元人民币,约合189011亿美元。
表3给出了以1986年可比价调整后2013年的产出45794.05亿元为基础,中国经济以6.5%—7.3%之间不同的新常态速度增长时,未来各年的总产出情况。对比表2和表3的结果,无论中国经济在这之间以什么样的新常态速度发展,在现有的生产水平(生产函数模式)和消费-投资模式下,单纯依靠资本投资的增长仍能维持中国经济发展到2024年。如果相对放慢发展速度则可持续发展到2025年。
表2和表3的结果带给我们两个主要信息:首先,从生产角度看,资本作为重要的投入要素,其积累增加对中国经济增长的红利促进作用还远远没有结束。在中国的现有生产能力下,即使单纯依靠资本存量增加,中国经济仍有可能维持以新常态速度发展8—10年。届时中国的产出水平能够达到2013年的2倍以上,近19万亿美元,将会很大地缩小与美国产出总值的距离(在美国经济正常发展的前提下);其次,理论角度可积累的稳态最大固定资本存量和相应的最大产出量都与很多因素和经济状态相关。包括代表生产能力的投入产出状态、投资占比状态和固定资本折旧状态等等,任何因素的改变,都会影响到可积累的固定资本存量的最大值及与其相关的最大产出。
四、结论与建议
作为重要的投入要素,资本投资对中国经济增长的促进作用是大家公认的,因此,资本红利未来能够持续刺激中国经济增长的时间是所有人共同关心的问题。现有的多数研究从资本逐利性角度、利用要素的边际报酬递减规律所得结论并不一致,更难回答资本红利未来的持续期问题。本文从资本投资积累的制约特征和路径规律角度进行探讨,论证了固定资本存量应该具有相对稳态的可积累最大值。并利用资本的永续存盘法和C-D生产函数模型,数理推导了固定资本存量最大值的条件约束公式。从而其他因素不变时,相应的产出也会有一个最大值。结合中国1986—2013年经济发展的数据,进行了实证估算。并预测了在新常态发展水平下,积累到最大资本存量中国经济能持续增长的时间。主要结论有如下几点:
首先,理论角度资本积累受到前期折旧和当期新增投资的影响,并且因为生产中投入要素具有边际报酬递减规律,以及新增投资受产出的约束等原因,固定资本存量的积累具有稳态条件最大值。
其次,假设固定资本存量满足永续存盘法,投入产出满足C-D生产函数,且投资占前期产出的确定比例时,数理推导出可积累的稳态条件固定资本存量最大值为:K t ≤[c t A t /(r t l t β )1/1-β +δ-1]1/β L t。其中很多影响因素都可以是时间的函数。当假设这些因素不随时间而改变时,该可积累的最大固定资本存量简化为。其中c、A、L、δ、和 β分别表示投资占前期产出的比例、全要素生产率水平、不变的劳动力总量、固定资本折旧率和劳动要素弹性系数。这说明该最大值与生产效率参数、投资占比和劳动力数量都是正相关关系,与固定资产折旧率和生产函数中劳动要素的弹性参数是负相关关系。
最后,以2001—2013年为中国当前经济状态样本进行拟合,估算得到能促进中国经济持续增长的最大固定资产存量约为1119531.31亿元(以1986年价格水平计算)。从而获得了对应该最大资本存量的最大产出,约为2013年产出水平的2.05倍。在新常态经济增长速度下,积累到最大固定资本存量,中国经济能持续发展到2024年,届时总产出约为19万亿美元,更加接近于美国当时的经济总量水平。
本文关于中国最大固定资本存量的讨论和估算是一种理想状态的动态极值,也是一种条件极值。称其为理想状态极值是指该极值是仅从固定资本存量积累规律角度获得,而直接认为该极值状态达到之前资本投资回报率没有降到0。事实上,投资回报率达到0或者固定资本存量积累到最大值都是资本投资停止增长的充分条件。而称其为条件极值指该极值的产生受到一些相关因素的影响,影响因素变化则极值变化。这些因素包括体现生产函数状态的劳动要素弹性参数和全要素生产率两因素。现有的国际经验和中国的实证研究都说明经济体在发展的过程中,要素弹性参数系数是具有一定的调整规律的。现实中劳动要素弹性参数系数和最大固定资本存量之间不是正向的相关关系,这会给实现经济增长和增加人们社会福利的两种不同目标分别带来什么样的影响值得被进一步关注。相关的极值影响因素还包括新增投资占前期产出的比例。虽然两者是正向的相关关系,但增加产出中与投资互补的消费比例,提高人们的生活水平和质量,是实现人们福利最大化的社会发展目标之一,这意味这需要降低投资占比。本文计算出来的当前经济状态下中国最大资本存量值是在新增投资占前期产出59.4%的情况下获得的。相对于欧美这样的发达国家,中国的投资占产出比例明显偏高。未来为了增加人们的福利,政府可能面临鼓励消费从而减少投资占比并影响最大可积累资本存量的矛盾,需要进行适当的协调。当然,现实中最大固定资本存量极值的发生还受其他因素的影响,包括劳动力总量水平和固定资本存量折旧率等。很多时候影响因素的客观变化方向和最大固定资本存量的积累方向不一致,需要进行具体权衡。但是,加强以下几方面的工作,可以达到从增加资本红利角度促进经济增长的目的:(1)加强生产函数中效率系数所代表的全要素生产率的增长。该增长不仅可以通过生产函数带来产出的直接增长,还可以通过匹配更多资本存量的方式增加可积累的最大固定资本存量值,从而实现间接促进经济增长的目的。(2)鼓励设备等固定资产的有效维护,减小折旧率。折旧率与最大固定资本存量之间有负相关关系,折旧率减小就可以使最大固定资产存量增加,从而增加其他条件不变时的最大产出量。(3)增加劳动力数量。作为缺一不可的两种投入要素之一,对劳动力数量的增加,也可以从间接增加最大可积累固定资本存量的角度对经济增长做出贡献。(4)加大到国外投资的力度。由于国内资本边际产出降低以及维持巨额固定资产总量也需要大量新增投资等原因,不如鼓励更多的资金走出去,投入到劳动力资源丰富而资本相对缺乏的周边国家和地区,能够获得比在中国更多的投资回报。
注释:略




