朋友们,大家好!天气越来越冷了,不少地方都下了雪,大家一定要注意身体哦!今天是2019年12月2日,数学世界继续和大家分享初中数学几何题。一些朋友希望猫哥多讲一些初中的数学题,所以这段时间就以讲解初中数学题为主。请朋友们先尝试自己做一做,再看解析过程,相信大家一定会有收获!
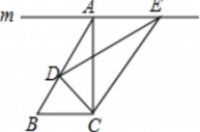
例题:(初中数学几何题)如图,已知在△ABC中,∠ACB=90°,过点A作直线m∥BC,过AB的中点D作DE⊥CD,DE交直线m于点E,连接CE,已知BC=5,AC=12,求AE的长.
这道题要求线段的长,对大多数学生来说,这道题的难度比较大,此题的考查知识点有平行线的性质、勾股定理、梯形中位线定理等知识。我们在做此题时,要认真观察图形,一定要认真分析条件之间有何关联,根据所求问题找出有用的解题线索。此题的给出的条件比较多,有一组平行线,多个直角三角形,还有一个中点,所以我们要充分利用这些条件。
解决此题的关键是由勾股定理得出方程,解方程即可得出结果。解题过程中要充分利用平行线的性质、作出梯形中位线并求出其长度。下面,猫哥就与大家一起来解决这道例题吧!
解答:取CE的中点F,连接DF,(原图没有画好,就不作辅助线了)
∵AE∥BC,D是AB的中点,
∴DF是梯形ABCE的中位线,
∴DF=1/2(BC+AE),
设DF=x,
∵BC=5,
∴AE=2x-5,
∵DE⊥CD,F是CE的中点,
∴CE=2DF=2x,
∵∠ACB=90°,AE∥BC,
∴∠CAE=90°,
在Rt△ACE中,
AE=2x-5,AC=12,CE=2x,
由勾股定理,得:
12^2+(2x-5)^2=(2x)^2,
解得:x=8.45,
∴AE=2×8.45-5=11.9,
即AE的长为11.9 .
(完毕)
温馨提示:由于此文是由原创作者猫哥一字一句打出来的,在电脑前待的时间长了,眼睛会有些干涩,所以文中难免会出现一些小错误,还请大家谅解!另外,若朋友们还有不明白的地方或者有更好的解题方法,欢迎留言参与讨论。谢谢!




